|
Question 1174984: Find a three-digit number such that the hundreds’ digit minus the tens’ digit is 1, the tens’ digit
minus the units’ digit is 1, and the sum of the digits is 15.
Found 3 solutions by math_tutor2020, ikleyn, MathTherapy:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
h = hundreds digit
t = tens digit
u = units digit
A three digit number like 789 means that h = 7, t = 8, u = 9
We can also construct that number like so
789 = 700+80+9
789 = 7*100+8*10+9*1
Going back to the general format, the three digit number 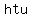 can be written as can be written as 
As another example, let's say
h = 5
t = 4
u = 2




In this very narrow context, the notation 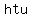 does not mean "h times t times u", even though with many algebra problems, we're conditioned to see two letters together and think "that's implied multiplication". does not mean "h times t times u", even though with many algebra problems, we're conditioned to see two letters together and think "that's implied multiplication".
With 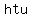 , I'm simply using three blank placeholders as the three digits. , I'm simply using three blank placeholders as the three digits.
Anyways, we're told that "hundreds’ digit minus the tens’ digit is 1" which means we can form the equation  . Solving for h gets us . Solving for h gets us 
We're also told that "the tens’ digit minus the units’ digit is 1" which forms  and that solves to and that solves to 
The two equations  and and  can be combined like so can be combined like so

 Replace t with 1+u Replace t with 1+u

So whatever the hundreds digit (h) is, we add on 2 to get the units digit (u).
-----------------------------------------
The last piece of useful information is that "the sum of the digits is 15". So the three digits add to 15.

 Plug in Plug in 

 Plug in Plug in  . Let's solve for the variable 'u'. . Let's solve for the variable 'u'.

 Subtract 3 from both sides Subtract 3 from both sides

 Divide both sides by 3 Divide both sides by 3
 This is the units digit This is the units digit
Once we know that, we can find the values of t and h


We have
h = 6
t = 5
u = 4
To check, we see that
h+t+u = 6+5+4 = 11+4 = 15
so that confirms the third equation and statement.
Also, we can see that the difference from the hundreds and tens digit (6 and 5) is 1 unit, so is the difference from the tens to the units digit. So the answer is fully confirmed.
Side note: you could use a trial and error process to guess three digit numbers, and see if you can land on the answer. But I think the algebraic method is most efficient.
------------------------------------------------
Answer: 654
Answer by ikleyn(52784)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Let x be the "ones" digit.
Then the "tens" digit is (x+1) and the "hundreds" digit is ((x+1)+1) = (x+2).
From the condition,
x + (x+1) + (x+2) = 15,
which implies
3x = 15 - 3 = 12
x = 12/3 = 4.
ANSWER. The number is 654.
Solved.
The problem is SO SIMPLE that the solution requires only several lines.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Find a three-digit number such that the hundreds’ digit minus the tens’ digit is 1, the tens’ digit
minus the units’ digit is 1, and the sum of the digits is 15.
Let tens digit be T
Then hundreds digit = 1 + T, and units digit = T - 1
Since they SUM to 15, we get: T + 1 + T + T - 1 = 15
3T = 15
Tens digit, or 
Hundreds digit is then: 1 + 5 = 6
Units digit is then: 5 - 1 = 4
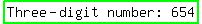
|
|
|
| |