Question 117487This question is from textbook glencoe algrbra 1
: dear godsend tutor first off i would like to thank you for helping me
now to business
my problem deals with solving eqautions in slope intercept form. this is the problem m=7/4x or 7 over 4-X ,b=2 Y=MX+b is slope intercept form this is what i got stuck on Y=7/4x+2 i have no idea what to do S.M!= save me !
sencerely raimius foulkes
This question is from textbook glencoe algrbra 1
Answer by solver91311(24713)   (Show Source): (Show Source):
You can put this solution on YOUR website! Raimius.
I don't have much of an idea what you want either. Everything you said was correct except that you specified the slope in terms of x. The slope is the coefficient of the x term when the equation is solved for y. (Solved for y means that y is on one side of the equal sign and everything else in the equation is on the other side, as opposed to standard form of the equation,  , point-slope form , point-slope form  , or two-point form , or two-point form , ,
In the point-slope form,  , y is the dependent variable, m (NOT mx) is the slope, x is the independent variable, and b is the y-intercept. , y is the dependent variable, m (NOT mx) is the slope, x is the independent variable, and b is the y-intercept.
Your equation should look like this:  or or  . I don't know what you mean by 'solving' this. There is no single solution for a single equation in two variables. You can choose any x value you like and there will be a corresponding y value. Any pair of values that satisfies the equation can be expressed as an ordered pair (x, y) that designates a point in . I don't know what you mean by 'solving' this. There is no single solution for a single equation in two variables. You can choose any x value you like and there will be a corresponding y value. Any pair of values that satisfies the equation can be expressed as an ordered pair (x, y) that designates a point in 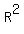 . The set of all such ordered pair solutions, and there are an infinite number of them, is a straight line. . The set of all such ordered pair solutions, and there are an infinite number of them, is a straight line.
If you needed a graph of this line, then it would look like this:
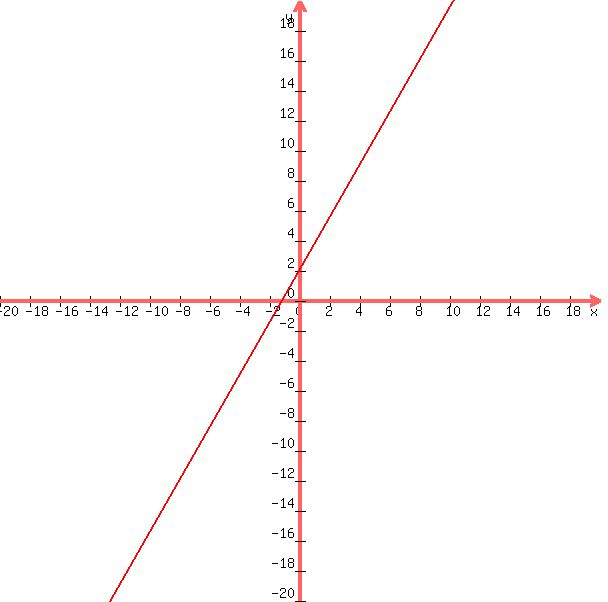
Now, if you happened to have a SECOND equation, one with a different slope number, THEN you could find a unique solution to the system of equations because the lines would intersect at one point and that would be your solution to the SYSTEM. The slopes have to be different, because lines with equal slopes are either parallel or co-incident giving you either no solutions or an infinite number of them.
Hope this helps,
John
|
|
|