|
Question 1174834: For a certain company, the cost function for producing x items is C(x)=50x+250 and the revenue function for selling x items is R(x)=−0.5(x−110)2+6,050. The maximum capacity of the company is 150 items.
The profit function P(x) is the revenue function R(x) (how much it takes in) minus the cost function C(x) (how much it spends). In economic models, one typically assumes that a company wants to maximize its profit, or at least make a profit!
Answers to some of the questions are given below so that you can check your work.
Assuming that the company sells all that it produces, what is the profit function?
P(x)=
What is the domain of P(x)?
Hint: Does calculating P(x) make sense when x=−10 or x=1,000?
The company can choose to produce either 60 or 70 items. What is their profit for each case, and which level of production should they choose?
Profit when producing 60 items =
Number
Profit when producing 70 items =
Number
Can you explain, from our model, why the company makes less profit when producing 10 more units?
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the cost function is c(x) = 50x + 250.
the revenue function is r(x) = -.5 * (x - 110) ^ 2 + 6050.
simplify this to get r(x) = -.5 * (x^2 - 220x + 12100) + 6050.
simplify further to get r(x) = -.5x^2 + 110x - 6050 + 6050.
this results in r(x) = -.5x^2 + 110x.
the profit function is p(x) = r(x) - c(x).
you get p(x) = r(x) - c(x) = -.5x^2 + 110x - (50x + 250).
the result is p(x) = -.5x^2 + 60x - 250.
your questions with answers are shown below.
QUSTION NUMBER 1:
Assuming that the company sells all that it produces, what is the profit function?
the profit function is p(x) = -.5x^2 + 60x - 250.
it is the result of the revenue function minus the cost function.
QUESTION NUMBER 2:
What is the domain of P(x)?
the value of x represents the number of items built and sold.
since the number of items built and sold can't be less than 0, than the minimum value of x is 0.
therefore, the domain of r(x) and c(x) and p(x) requires all values of x to be greater than or equal to 0.
when x = 0, r(x) = -.5x^2 + 110x becomes r(x) = 0.
this is ok, since you never want the revenue to become less than 0, so the value of x can be equal to 0 without violating that requirement.
when x = 0, c(x) = 50x + 250 becomes c(x) = 250.
250 becomes the fixed cost.
it costs the company that much regardless of how many items they build and sell.
the incremental cost per item built is equal to 50.
the incremental cost changes depending on the number of items built.
when x = 0, p(x) = -.5x^2 + 60x - 250 = -250.
the profit is negative 250.
a negative profit is a loss.
when 0 items are built and sold, the company takes a loss of 250.
that's to be expected since there is a fixed cost of 250 that remains the same regardless of how many items are built and sold.
the breakeven point is when p(x) = 0.
when p(x) = 0, the revenue is equal to the cost.
to solve for that, set p(x) = 0 in the equation of p(x) = -.5x^2 + 60x - 250.
the equation becomes -.5x^2 + 60x - 250 = 0
factor that quadratic equation to get:
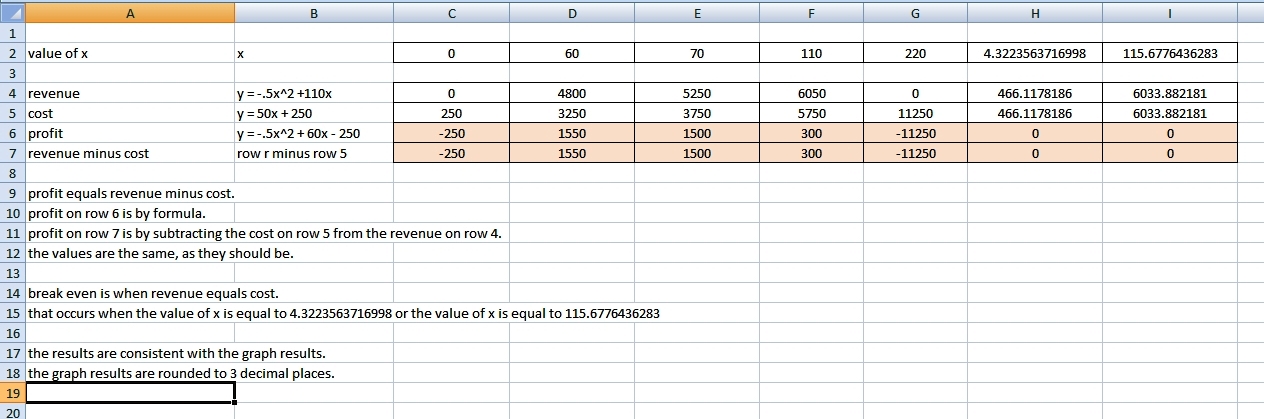
x = 4.3223563716998 or x = 115.6776436283
QUESTION NUMBER 3:
Does calculating P(x) make sense when x=−10 or x=1,000?
x represents the number of units built and sold.
as such, the value of x cannot be negative.
therefore x = -10 doesn't make any sense.
when x = 1000, the revenue is negative.
as such, the value of x cannot be negative.
therefore x = 1000 doesn't make any sense.
QUESTION NUMBER 4:
The company can choose to produce either 60 or 70 items.
What is their profit for each case, and which level of production should they choose?
Profit when producing 60 items = 1550.
Profit when producing 70 items = 1500.
QUESTION NUMBER 5:
Can you explain, from our model, why the company makes less profit when producing 10 more units?
the profit is less when 70 units are built and sold because the costs per unit are rising faster than the revenue per unit.
this can be seen in the graph.
the revenue increase from 60 units to 70 units is equal to 450.
the cost increase from 60 units to 70 units is equal to 500.
here's the graph.
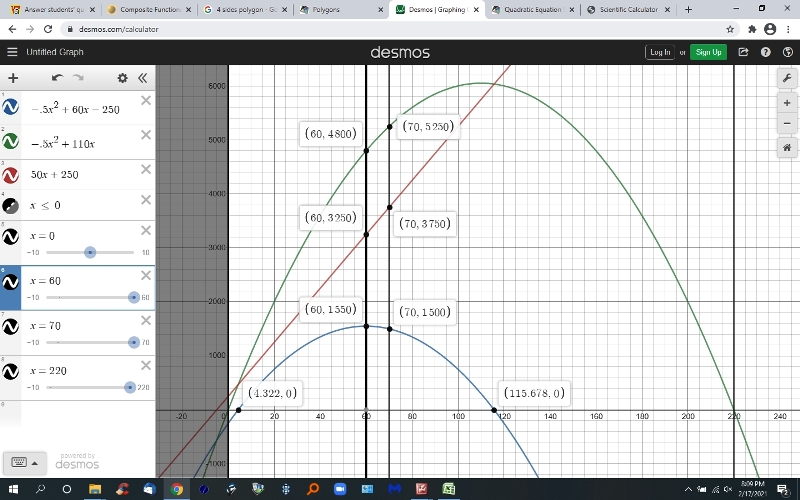
here's the excel spreadsheet that shows the key numbers.
i'll be available to answer any questions you might have about this.
on the graph, the green is the revenue function, the blue is the profit function, and the red is the cost function.
theo
|
|
|
| |