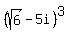SOLUTION: Use DeMoivre's Theorem to find the indicated power of the complex number. Write the result in standard form. {{{(sqrt(6)-5i)^3}}}

We draw the graph of the complex number  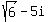which is the vector whose tail
is at the origin (0,0) and whose tip is at the point (√6,-5). The length of
that vector is called r.



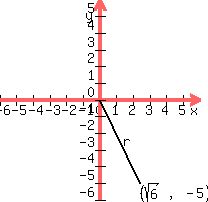Then we draw a perpendicular from (√6,-5) to the x-axis:



we have a right triangle so the angle measured counter-clockwise
from the right side of the x-axis, indicated by the red arc. We
use the calculator to determine that tan-1(y/x)=tan-1(-5/√6)=-63.89986122
and we add 360° to get it positive θ=296.1001388°. 

We also use the Pythagorean theorem to find r:

  
                                                        __
The terminal side of any angle is always positive so r=√31.



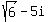
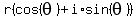
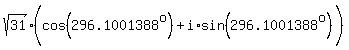Next we use DeMovre's theorem to raise everything to the 3rd power, which
means we raise the r to the 3rd power and multiply the θ by 3:





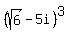
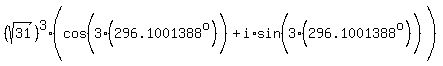
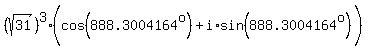Use your TI-84 or TI-83 with MODE DEGREE and MODE a+bi

-169.0147923+34.99999984i

The easy way would be not to bother with DeMoivre's theorem and just type in
(√(6)-5i)^3 with MODE set at a+bi, where the key for i is gotten by pressing
2nd then the decimal or period key which is the key in the middle at the very
bottom row of keys on your calculator.  You'd get -169.0147923+35i, but your
teacher specifies that you must use DeMovre's theorem.  So you have to go
through all that above. 

Edwin