Question 1174562: Choose a new vehicle sold in the United States in November 2014 at random. The probability distribution for the type of vehicle chosen is given below.
Vehicle type and Probability:
Passenger Car 0.46 - Pickup Truck 0.15 - SUV 0.10 - Crossover ? - Minivan 0.05
1) What is the probability that the vehicle is a crossover?
2) Given that the vehicle is not a passenger car, what is the probability that it is a pickup truck?
3) What is the probability that the vehicle is a pickup truck, SU, or minivan?
Using the same information as the last question. Suppose you select 3 vehicles at random. You want to know the probability that the vehicles are of three different types. Describe how you would carry out a simulation to help answer this question. Do not actually perform the simulation.
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi
Passenger Car 0.46 - Pickup Truck 0.15 - SUV 0.10 - Crossover .24 - Minivan 0.05
P(crossover) = 1 - .46 -.15 - .10 - .05 = .24
P(pickup|Not car) = .15/.54
P(pickup truck, SU, or minivan) = .15 + .10 + .05
Select 3: the probability that the vehicles are of three different types
Yes, 5C3 0r 10 ways of selecting a trio from 5 types.
&
P(of each trio)... would be the product of their individual probabilities
Total Probability(vehicles are of three different types) would be the sum of
each of the possible trios.
Wish You the Best in your Studies.
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
The solution by @ewatrrr to the last question is ABSOLUTELY WRONG.
Below see my correct solution.
Let the letters mean
P - passenger car
T - truck
S - SUV
C - crossover
M - Minivan.
Then the probability under the last question is the sum of 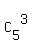 = 10 addends
p = p(PTS) + p(PTC) + p(PTM) + p(TSC) + p(TSM) + p(SCM) + . . .
where all combinations of 5 letters taken 3 at a time are used.
Each p(XYZ) is the product of the 3 (three) relevant given probabilities.
So, according to the problem's instruction, I do not calculate, but only EXPLAIN how to build the calculation formula.
|
|
|
