SOLUTION: (a) Find a cubic polynomial with integer coefficients that has (cube root of 2) + (cube root of 4) as a root. (b) Prove that the (cube root of 2) + (the cube root of 4) is irr

Let r =  + .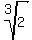


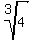Then,  since  (a+b)^3 = a^3 + 3a^2b + 3ab^2 + b^3 = a^3 + 3ab*(a+b) + b^3


    r^3 =  + . +  =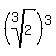 

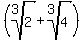        = 2 + 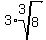. 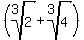+ 4 = 2 + 3*2*r + 4 = 6 + 6r.


It means that  r = 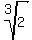 +  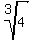 is the root to this equation


    r^3 - 6r - 6 = 0.      (*)


ANSWER. 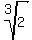   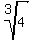+   is the root of the cubic polynomial  x^3 - 6x - 6.

In part (a), I proved that the number  r = 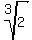 +  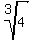 is the root of the cubic equation


    x^3 - 6x - 6 = 0.     (**)


Therefore, due to the Rational root theorem, if the number "r" is rational, it must divide the constant term of 6, 
i.e. r must be one of the numbers +/-1, +/-2, +/-3, +/-6.


But it is easy to check that no one of these divisors of 6 IS NOT THE ROOT to equation (**).


Indeed, for these values of x, the values of the polynomial  f(x) = x^3 - 6x -6  are given in the Table


    x       -1      1     -2      2     -3      3     -6     6

    f(x)    -1    -11     -2    -10    -15      3    -186   174


and no one of these values of the polynomial  f(x)  is equal to  0  (zero).