Question 1174166: A biology teacher drives from Naperville over the Cleveland to visit her sister. During the trip there, she travels the first half of the time at 65 km/hr and the second half the time at 95 km/hr. When she comes back, she drives the first half the distance at 65 km/hr and the second half of the distance at 95 km/hr. What is her average speed coming back from Cleveland?
I am confused how to calculate this. I thought it might just be the average of the two speeds but that is not the correct answer. Also, I tried to set up an equation, but solving this did not give me the right answer. The equation I thought might work (wrong answer of 78.6 km) was D/160 + D(1/260 + 1/380), and then divided 1 by 0.0127 (sum of all the D terms). Any help would be greatly appreciated. Thank you.
Answer by ikleyn(52803)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
A biology teacher drives from Naperville over the Cleveland to visit her sister.
During the trip there, she travels the first half of the time at 65 km/hr and the second half the time at 95 km/hr.
When she comes back, she drives the first half the distance at 65 km/hr and the second half of the distance at 95 km/hr.
What is her average speed coming back from Cleveland?
~~~~~~~~~~~~~
Solution
Let " t " be her total time driving from N to C.
Then the total distance from N to C is d = 0.5t*65 + 0.5t*95 = 0.5t*(65+95) = 0.5t*160 = 80t kilometers.
Half the distance is 40t kilometers.
When driving back (from C to N), the total driving time is T = 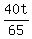 + + 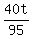 hours. (1)
The average speed driving back is the total distance 80t divided by the total time of the formula (1), i.e. hours. (1)
The average speed driving back is the total distance 80t divided by the total time of the formula (1), i.e.
 = = 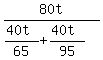 = = 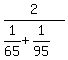 = 77.1875 kilometers per hour. ANSWER = 77.1875 kilometers per hour. ANSWER
Solved.
------------
Is everything clear to you in my solution ?
When you complete read it, do not forget to post your "THANKS" to me for my teaching.
///////////////
For the problem, it does not matter, who is the driver: "biology teacher", or carpenter, or sales manager, or astronaut,
or vice-president, or anybody else.
Therefore, naming his (or her) specialty is IRRELEVANT to the problem.
I know that 80% of problems in US Math textbooks are formulated this way.
It is NOT an argument that they all are correct; they all are WRONG.
They teach young students to think incorrectly, and, in addition, they treat the students inadequately . . .
As a result, when such a student sees the words "vice-president" instead of "biology teacher",
he (or she) thinks that it is another problem . . .
|
|
|