Question 1174136: While playing mini golf, you hit the ball off of a wall to attempt at making it in the hole. The ball is located at (5,4) and the hole is located at (9,8). The point where the ball hits the wall is (7,0). Write an equation for the path of the ball and then determine if you will make your putt. Vertex formula must be used.
I have tried this problem a different way and discovered that the putt is not made. I also know that I should substitute the vertex, (7,0) for (h,k). If I substitute the first coordinate, (5,4) into this equation believe I use 5 for the x value and 4 for the y value, resulting in "a=1". If I do the same thing again with the other coordinate "a=2" I am not sure how I am supposed to be looking at this to determine whether or not the putt missed.
Found 2 solutions by Boreal, greenestamps:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! Given the vertex is (7, 0) the equation is f(x)=a(x-7)^2+0
f(5)=4=a(-2)^2+0 and a=1 as you found.
The vertex is symmetrical around the line x=7, so (5, 4) and (9, 4) are points, so you wouldn't make the putt. What you want to know is given the equation, does (9 ,8) lie on the line? It doesn't.
also f(9)=2^2+0 so (9, 4) would be the ball's position.

Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The golf ball does not follow a parabolic path; it follows the graph of an absolute value function.
With vertex (7,0) and starting point (5,4), the slope of the first part of the path is -2, so the equation is 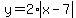
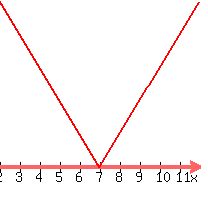
The change in x from the starting point to the vertex (5 to 7) is the same as the change in x from the vertex to the target (7 to 9). Because of the symmetry of the absolute value function, the y value at x=9 will be the same as it is at x=5; so at x=9 the position of the ball will be (9,4). So the ball will not hit the target at (9,8).
--------------------------------------------------------
Alternative solution method....
Since the ball follows the path of an absolute value function, the slope of the path from the vertex (wall) to the target should be the opposite of the slope from the starting point to the vertex.
But the slope from the starting point to the wall is -2; the slope from the wall to the target is 4.
So again the answer is that the ball will not hit the target.
|
|
|