Question 1173843: How many distinct permutations can be made from the letters of the word "PROPORTION"?
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
10 letters; of which there are 3 O's, 2 P's, and 2 R's.
By a basic counting principle....
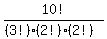
Use a calculator if a numerical answer is needed.
Note that the general principle is that the number of arrangements is the factorial of the total number of letters, divided by the factorials of the numbers of times each letter is repeated.
Using that general principle, the problem can be seen this way:
10 letters; of which there are 3 O's, 2 P's, 2 R's, 1 T, 1 I, and 1 N.
And the number of arrangements is
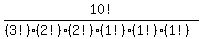
Of course the result is the same, since the factors of 1! do not alter the final answer.
|
|
|