Question 1173837: The rate of a small aircraft in calm air is 125 mph. If the wind is currently blowing south at a rate of 5 mph, how far north can a pilot fly the plane and return it within 4 h?
Found 2 solutions by Boreal, ikleyn:
Answer by Boreal(15235)   (Show Source): (Show Source):
You can put this solution on YOUR website! goes north at 120 mph for x hours
goes back south at 130 mph for 4-x hours
Those distances are equal
so 120x=520-130x units are miles/hr *hr or miles
250x=520
x=2.08 hours north or 249.6 miles
Answer by ikleyn(52781)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Below I explain how this problem has to be solved, actually.
How it SHOULD be solved and how it is EXPECTED to be solved.
Watch my steps (!)
It flights WITH the wind at the effective speed of 125 + 5 = 130 mph
and AGAINST the wind at the effective speed of 125-5 = 120 mph.
Let "d" be this distance, the problem asks for.
Time spent WITH the wind is 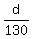 hours.
Time spent AGAINST the wind is hours.
Time spent AGAINST the wind is 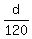 hours.
The total time equation is hours.
The total time equation is
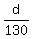 + + 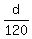 = 4 hours (given).
You just completed the setup, and just have an equation to solve.
To solve it, multiply both sides (everything by 120*130. You will get
120d + 130d = 4*120*130,
which gives you
d = = 4 hours (given).
You just completed the setup, and just have an equation to solve.
To solve it, multiply both sides (everything by 120*130. You will get
120d + 130d = 4*120*130,
which gives you
d = 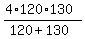 = 249.6 miles.
ANSWER. How far North is 249.6 miles. = 249.6 miles.
ANSWER. How far North is 249.6 miles.
You are very happy person, because you got now from me
the best possible solution with detailed explanations.
Such a solution with explanations you will get NOWHERE ELSE.
-------------
Using "time" equation is a STANDARD method of solving such problems.
From this lesson, learn on how to write, how to use and how to solve a "time" equation.
To see many other similar solved problems, look into the lessons
- Had a car move faster it would arrive sooner
- How far do you live from school?
- Earthquake waves
- Time equation: HOW TO use, HOW TO write and HOW TO solve it
in this site.
/\/\/\/\/\/\/\/
By the way, the solution by @Boreal is formally INCORRECT.
|
|
|