Question 1173754: Hi,
I'm really confused on how to solve complex higher-degree polymials, especially one like this with really large values:
8x^4-92x^3+342x^2-513x+270
My textbook tells me to use the rational root theorem, but it's too time-consuming to test out all the different root possibilities, and the grouping method also didn't work for me.
Thanks for your help :)
Found 3 solutions by ikleyn, ewatrrr, MathTherapy:
Answer by ikleyn(52756)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
To save your time, make a plot of a polynomial to find/identify its integer roots.
You may use your graphing calculator.
Or use this free of charge plotting tool at the Internet site
www.desmos.com
Also, if you have Excel as a part of the Office software in your computer,
you can make a list of the potential roots, using the Rational root theorem,
then to program the formula in Excel to calculate the polynomial value for one single root,
and then to expand your calculations to all other potential roots from the list.
.................
As the last tool against this malignant polynomial, try this Internet (free of charge) solver
https://www.mathportal.org/calculators/polynomials-solvers/polynomial-roots-calculator.php
Input the polynomial there and get the answer in seconds with complete, professional and very COMFORTABLE explanations.
Yes, it is assumed that the students should use the Rational root theorem,
but this concrete task is extremely time consuming (I'd say, tooooo excessively and unjustly time consuming).
So, if you know the Rational root theorem and are able to apply it in simple cases, it is just enough for your education.
Making mechanical work will add nothing essential to your skills.
I am saying it to justify your using of this online solver.
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
Would recommend having the technology to do graphing:
https://www.padowan.dk/download/ is a FREE graph software & Easy to use.
One can copy/paste the polynomial under 'function',
the software graphs the function and one can then determine
the zeros by clicking where the curve crosses the x-axis.
It also serves as a great tool for entering values into the function.
On this one: f(x) =(x-1.5)(x-1.5)(x-2.5)(x-6)
Wish You the Best in your Studies.
Answer by MathTherapy(10549)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hi,
I'm really confused on how to solve complex higher-degree polymials, especially one like this with really large values:
8x^4-92x^3+342x^2-513x+270
My textbook tells me to use the rational root theorem, but it's too time-consuming to test out all the different root possibilities, and the grouping method also didn't work for me.
Thanks for your help :)
Now, I do agree that it's quite tedious to use the RATIONAL ROOT THEOREM to find roots and then factors from those roots, but in this case,
after trying a few of the SMALLER FACTORS of the constant, "+ 270", such as ± 1, ± 2, ± 3, and ± 5, we find that 6 is a ROOT, and so, x - 6 is a FACTOR.
In this case, just 8 integers were tried before a ROOT (+ 6) was derived. We now use this factor, x - 6, and long division of polynomials to find the
other POLYNOMIAL factor, as follows: 8x^3 - 44x^2 + 78x - 45
x - 6)8x^4 - 92x^3 + 342x^2 - 513x + 270
8x^4 - 48x^3
- 44x^3 + 342x^2
- 44x^3 + 264x^2
78x^2 - 513x
78x^2 - 468x
- 45x + 270
- 45x + 270
0By the way, if you know about SYNTHETIC DIVISION, you can also use that to find the QUOTIENT above.
So far, we have:  .
The FACTORING gets a little easier now, since the INTEGER ROOTS, based on the constant, - 45, are: ± (1, 3, 5, 9, 15, 45). Now, since none of these INTEGERS are ROOTS, the other roots MUST be fractional!
We now try for FRACTIONAL ROOTS, based on the factors of the constant (- 45), and “A”, the LEADING COEFFICIENT, as follows: .
The FACTORING gets a little easier now, since the INTEGER ROOTS, based on the constant, - 45, are: ± (1, 3, 5, 9, 15, 45). Now, since none of these INTEGERS are ROOTS, the other roots MUST be fractional!
We now try for FRACTIONAL ROOTS, based on the factors of the constant (- 45), and “A”, the LEADING COEFFICIENT, as follows:
 Notice that “1” was NOT USED as a factor of “A” since that leads to an INTEGER, which we’ve already established, does not provide a ROOT.
Once again, trying the fractions,
Notice that “1” was NOT USED as a factor of “A” since that leads to an INTEGER, which we’ve already established, does not provide a ROOT.
Once again, trying the fractions, 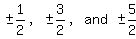 , we find that , we find that  are ROOTS, which means that are ROOTS, which means that  , resulting in the factors: , resulting in the factors: 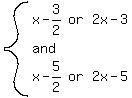 From factors 2x - 3 and 2x - 5, we FOIL to get the trinomial: 4x2 - 16x + 15.
We now use this as the DIVISOR to determine the other FACTOR(S) of the trinomial, 8x3 - 44x2 + 78x - 45. This is shown below!
And remember, again you could also use SYNTHETIC DIVISION to determine the QUOTIENT below.
From factors 2x - 3 and 2x - 5, we FOIL to get the trinomial: 4x2 - 16x + 15.
We now use this as the DIVISOR to determine the other FACTOR(S) of the trinomial, 8x3 - 44x2 + 78x - 45. This is shown below!
And remember, again you could also use SYNTHETIC DIVISION to determine the QUOTIENT below.
2x - 3
4x2 - 16x + 15)8x^3 - 44x^2 + 78x - 45
8x^3 - 32x^2 + 30x
- 12x^2 + 48x - 45
- 12x^3 + 48x - 45
As shown above, the final FACTOR is the above QUOTIENT, 2x - 3, which is actually a multiple factor.
Therefore, we get the  . .
|
|
|