Question 1173739: Prove that quadrilateral A(1,-2), B(13,4), C(6,8) and D(-2,4) is a trapezoid, but is not an isosceles trapezoid.
Found 2 solutions by greenestamps, ewatrrr:
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Proving two sides parallel makes it a trapezoid. A rough sketch of the four points shows that probably sides AB and CD are parallel. Confirm that by showing their slopes are equal.
Then showing that sides AD and BC are different lengths proves that the trapezoid is not isosceles. That is easily shown using the distance formula.
You can do the simple calculations....
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,

m =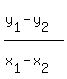
A(1,-2) C(6,8)
B(13,4), m = -6/-12 = 1/2 * D(-2,4), m = 4/8 = 1/2 *
AB is parallel to CD as the slopes of these two sides segments are equal.
Two sides of the quadrilateral are parallel: it is a trapezoid
distance A(1,-2) to D(-2,4) is 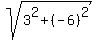 = √45 D = = √45 D = 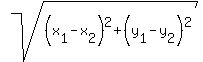
distance B(13,4) to C(6,8) is 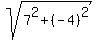 = √65 = √65
AB and BC are NOT the same length- is not an isosceles trapezoid.
|
|
|