Question 1173711: Outside temperature over a day can be modeled as a sinusoidal function. Suppose you know the temperature is 75 degrees at midnight and the high and low temperature during the day are 85 and 65 degrees, respectively. Assuming t is the number of hours since midnight, find an equation for the temperature, D, in terms of t.
D(t)=
Found 2 solutions by ikleyn, htmentor:
Answer by ikleyn(52903)   (Show Source):
You can put this solution on YOUR website! .
D(t) = 75 - 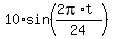 degrees.
The amplitude 10 is half the difference 85-65.
75 degrees is the mean temperature, and it happens precisely at midnight - so the sine function has no time shift.
The period is 24 hours.
------------
PLEASE pay ATTENTION that the sign before the sine function in my post is " - " (MINUS), as it should be,
in opposite to the post by @htmentor, where the sign before the sine function is " + ", which is WRONG.
It is of significant IMPORTANTCY (!)
In this problem, to miss these signs has the same effect as to miss a day and a night.
Answer by htmentor(1343)  (Show Source):
You can put this solution on YOUR website! The temperature at time t=0 (midnight)is 75 degrees, and the temperature
oscillates over a range of +/- 10 degrees during a 24 hour period.
Thus the amplitude of oscillation is 10, and the midline temperature is 75.
A complete cycle of 2pi takes place over 24 h, so the "angular frequency" is
w = 2pi/24 = pi/12
So the equation is D(t) = 10sin((pi/12)*t) + 75
|
|
|
