Question 1173558: A quadratic function has zeros −3 and 5 and contains the point (4, 14). Find the equation of the
quadratic function in standard form
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source):
You can put this solution on YOUR website!
Hi,
A quadratic function has zeros −3 and 5 and contains the point (4, 14).
f(x) = a(x+3)(x-5)
14 = a(7)(-1)
-2 = a
f(x) = -2(x+3)(x-5) = -2(x^2-2x-15)
f(x) = -2x^2 + 4x + 30
Wish You the Best in your Studies.
Answer by ikleyn(52786)  (Show Source):
You can put this solution on YOUR website! .
A quadratic function has zeros −3 and 5 and contains the point (4, 14). Find the equation of the
quadratic function in standard form
~~~~~~~~~~~~~~~~
From the condition, you can write this quadratic function in the form
q(x) = a*(x-(-3))*(x+5) = a*(x+3)*(x-5) (*)
with unknown real coefficient "a".
Notice that in this form, the function q(x) has the zeros at -3 and 5, as prescribed.
Now, to find the unknown coefficient "a", use the condition, that its plot contains the point (4,14).
It means that the value of q(4), when you substitute x= 4 in it, is 14
14 = a*(4+3)*(4-5), or
14 = -7a,
a = 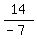 = -2.
Therefore, the function q(x) is q(x) = -2(x+3)*(x-5)}}}.
You may convert it further to the standard form q(x) = -2x^2 + 4x + 30. ANSWER
Solved.
|
|
|
