Question 1173392: In a school, every grade 10 student need to study 7 subjects out of 14. It is given that 4 of them are core subject, and the rest are optional. How many arrangements of the subjects are available for the students?
Found 2 solutions by CPhill, ikleyn:
Answer by CPhill(1959)   (Show Source): (Show Source):
You can put this solution on YOUR website! Here's how to solve this problem:
**1. Choose the Optional Subjects:**
* Since 4 subjects are core, the students need to choose 3 more subjects from the remaining 10 optional subjects.
* The number of ways to choose 3 optional subjects from 10 is given by the combination formula:
* ¹⁰C₃ = 10! / (3! * 7!) = (10 * 9 * 8) / (3 * 2 * 1) = 120
**2. Arrange the Chosen Subjects:**
* Once the 7 subjects are chosen (4 core and 3 optional), they can be arranged in 7! ways.
* 7! = 7 * 6 * 5 * 4 * 3 * 2 * 1 = 5040
**3. Calculate the Total Number of Arrangements:**
* To find the total number of arrangements, multiply the number of ways to choose the optional subjects by the number of ways to arrange them:
* Total arrangements = ¹⁰C₃ * 7! = 120 * 5040 = 604800
**Therefore, there are 604,800 possible arrangements of the subjects for the students.**
Answer by ikleyn(52832)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
In a school, every grade 10 student need to study 7 subjects out of 14.
It is given that 4 of them are core subject, and the rest are optional.
How many arrangements of the subjects are available for the students?
~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Based on the context, my common sense says me that this problem is about combinations,
and not about permutations, as @CPhill calculates and treats it.
So, I solve it differently, and my answer is different from that by @CPhill.
Every student must take 4 core subjects, and a student should take 3 additional subjects, selecting them
from 14-4 = 10 remaining optional subjects.
So, the total number of all possible combinations is 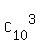 = = 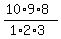 = 120. ANSWER = 120. ANSWER
Solved. The order of subjects in arrangements does not matter.
I am 137% sure that the treatment by @CPhill is not that the problem does require.
|
|
|