Question 1173375: A small manufacturing makes and sells x machines each month. The monthly cost, C ,in dollars, of making x dollars is given by
C(x)= 0.35x^2 + 3200
The monthly revenue, R, in dollars, obtained by selling x machines is given by
R(x)= 180x - 0.55x^2
If the company does maximum profit what is the selling price of each machine?
Found 2 solutions by CubeyThePenguin, ikleyn:
Answer by CubeyThePenguin(3113)   (Show Source):
You can put this solution on YOUR website! Profit is revenue minus cost.
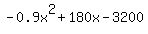
The maximum is at -b/2a = 100.
The selling price of every machine is R(x) divided by x, or 125 dollars.
Answer by ikleyn(52803)  (Show Source):
You can put this solution on YOUR website! .
Your formulation is FATALLY WRONG,
and I came to fix it.
See my editing below.
A small manufacturing makes and sells x machines each month. The monthly cost, C ,in dollars,
of making x  MACHINES is given by
C(x)= 0.35x^2 + 3200
The monthly revenue, R, in dollars, obtained by selling x machines is given by
R(x)= 180x - 0.55x^2
If the company does maximum profit what is the selling price of each machine?
|
|
|
