SOLUTION: Find four consecutive even integers such that three times the sum of the first and third numbers is equal to four times the sum of the second and fourth numbers.

Algebra ->  Average -> SOLUTION: Find four consecutive even integers such that three times the sum of the first and third numbers is equal to four times the sum of the second and fourth numbers.       Log On


   

Question 1173284: Find four consecutive even integers such that three times the sum of the first and third numbers is equal to four times the sum of the second and fourth numbers.

Found 3 solutions by ikleyn, greenestamps, ewatrrr:
Answer by ikleyn(52834) About Me  (Show Source):
You can put this solution on YOUR website!
.

The numbers are n, (n+2), (n+4) and (n+6), in ascending order.


The equation is


    3*(n + (n+4)) = 4*((n+2) + (n+6))


Simplify


    3*(2n+4) = 4*(2n+8)

    6n + 12  = 8n + 32

    12 - 32  = 8n - 6n

      -20  =   2n

        n  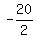=  -20%2F2 = -10.


ANSWER.  The numbers are -10, -8, -6, -4.

Solved, answered and explained.



Answer by greenestamps(13203) About Me  (Show Source):
You can put this solution on YOUR website!


Let the four consecutive even integers be x, x+2, x+4, and x+6.

Three times the sum of the first and third is equal to four times the second and fourth:

3%28x%2B%28x%2B4%29%29+=+4%28%28x%2B2%29%2B%28x%2B6%29%29
3%282x%2B4%29+=+4%282x%2B8%29
6x%2B12+=+8x%2B32
2x+=+-20
x+=+-10

ANSWER: -10, -8, -6, and -4

Answer by ewatrrr(24785) About Me  (Show Source):
You can put this solution on YOUR website!

Hi  
four consecutive even integers: n , (n+2), (n+4), (n+6)
three times the sum of the first and third numbers 
is equal to four times the sum of the second and fourth numbers. 
3(n + (n+4)) = 4((n+2) + (n+6))
3(2n+4) = 4(2n+8)
6n + 12 = 8n + 32
 -20 = 2n
n = -10
four consecutive even integers are:  -10, -8, -6, -4 
Checking our Answer:
3(-16) = 4(-12) = 48  checks!
Wish You the Best in your Studies.