|
Question 1173231: Two boats leave a harbour at the same time and head out at an angle of 35o to each other. Boat A is travelling at 45 km/h and boat B is travelling at 52 km/h. How far apart are the two boats after two hours?
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
Two boats leave a harbour at the same time and head out at an angle of 35o to each other
Boat A is travelling at 45 km/h and boat B is travelling at 52 km/h.
How far apart are the two boats after two hours?
Viewing the boats traveling forming a Right Triangle ∠A = 35°

one boat travels 90m (along b), the other 104m(along c)
Distance apart will be a on the picture
C^2 = a^2 + b^2
(104)^2 = a^2 + (90)^2
10816= a^2 + 8100
10816 - 8100 = a^2
2716 = a^2
a = 52.115km
Assuming the travel would result in a Right Triangle may not be the case:
Yes, Best to use cosine Law to cover all the bases.
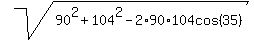 = 62.234km = 62.234km
In this case, travel didn't end up representing the model of a right Triangle.
Wish You the Best in your Studies.
Answer by ikleyn(52776)   (Show Source): (Show Source):
You can put this solution on YOUR website! Two boats leave a harbour at the same time and head out at an angle of 35o to each other.
Boat A is travelling at 45 km/h and boat B is travelling at 52 km/h.
How far apart are the two boats after two hours?
~~~~~~~~~~~~~~~~~~~
The problem is to find the third side of a triangle, given its two sides and the angle between them.
It is based on using the cosine law. The Pythagorean formula, used by @ewatrrr, is IRRELEVANT.
One side of the triangle is the traveled distance by boat A: it is a = 45*2 = 90 km.
Over side of the triangle is the traveled distance by boat B: it is b = 52*2 = 104 km.
The third side, according to the cosine law, is
d = 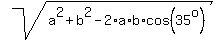 = = 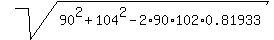 = 62.234 km.
ANSWER. In two hours, the boats are 62.234 km apart. = 62.234 km.
ANSWER. In two hours, the boats are 62.234 km apart.
Solved.
--------------
Do not accept any different answer.
Ignore the post by @ewatrrr, since her solution is INCORRECT.
|
|
|
| |