Question 1173074: Your aunt purchased a home for $375,000. After a 20% down payment, the balance was financed with a 30-year, 3.1% fixed-rate mortgage.
Prepare an amortization schedule for the first three month of your aunt's loan.
I was just able to get the down payment: 375,000 x .20 = 75,000
Found 2 solutions by ewatrrr, Theo:
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi
$375,000, $75,000 down, 30yr 3.1 fixed rate
Mo pmt Balance Ppd Int I tot
1 $1,347 $299,528 $472 $875 $875
2 $1,347 $299,054 $474 $874 $1,749
3 $1,347 $298,579 $475 $872 $2,621
Many Calculators online,following referenced
https://www.usbank.com/home-loans/mortgage/mortgage-calculators/fixed-rate-calculator.html
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! the purchase price was 375,000.
20% down would be equal to .2 * 375,000 = 75,000
subtract that from 375,000 to get 300,000 that has to be financed.
the interest rate on the mortgage is 3.1% per year.
divide that by 100 to get the interest rate on the mortgage is .031 per year.
divide that by 12 to get the interest rate on the mortgage is .031/12 per month.
use a financial calculator to find out what the payments need to be at the end of each month of the loan.
the inputs to the calculator will be:
present value (pv) = -300000
future value (fv) = 0
number of time periods = 30 years * 12 months per year = 360 months.
interest rate per time period = (3.1/12)% per month.
the payments will be made at the end of each time period.
using my ti-ba-ii business analyst financial calculator, i get a payment of 1281.049197 at the end of each of the 360 months.
using the online financial calculator found at https://arachnoid.com/finance/index.html, i get the same answer.
the results of using that calculator are shown below:
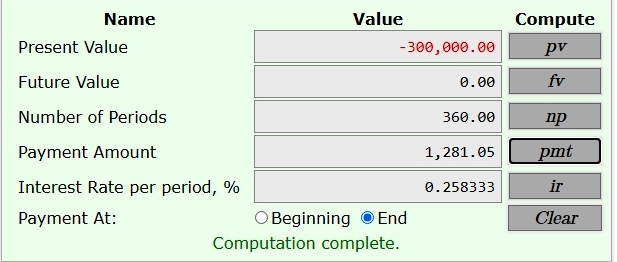
once you have the monthly payment, you can prepare the amortization schedule for the first 3 months.
at end of month 0, your remaining balance is 300,000
at end of month 1, you multiply 300,000 * (1 + .031/12) to get 300775.
you then subtract the payment of 1281.049197 from that to get a remaining balance of 299493.9508.
at the end of month 2, you multiply 299493.9508 * (1 + .031/12) to get 300267.6435.
you then subtract the payment of 1281.049197 from that to get a remaining balance of 298986.5943..
at end of month 3, you multiply 298986.5943 * (1 + .03/12) to get 299758.9763.
you then subtract the payment of 1281.049197 from that to get a remaining balance of 298477.9272.
i prepared an excel spreadsheet that details these calculations from the first few months of the loan to the last few months of the loan to show you how the loan progresses from start to finish, with the middle months left out so the presentation doesn't become too large.
here's the display of the excel spreadsheet analysis.
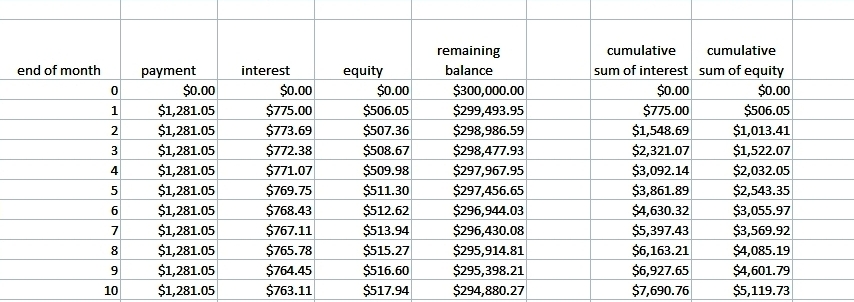
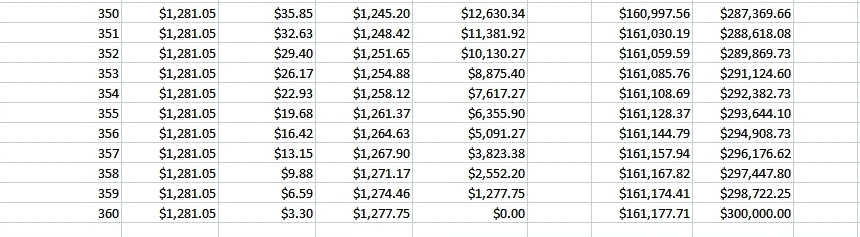
the spreadsheet rounds the displays to the nearest penny, but the calculations are done with the unrounded numbers.
|
|
|