SOLUTION: What is the smallest integer which multiplied by 40 gives a perfect square?

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: What is the smallest integer which multiplied by 40 gives a perfect square?      Log On


   

Question 1173053: What is the smallest integer which multiplied by 40 gives a perfect square?
Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.

Decomposition of the integer number of 40 into the profuct of prime integers is


    40 = 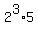2%5E3%2A5.


From this decomposition, it is clear that the number which multiplied by 40 gives a perfect square is 2*5 = 10.


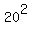Indeed,  10*40 = 400 = 20%5E2.


Also, it is clear from the decomposition, that 2*5 = 10 is the MINIMAL integer number with such a property.

Solved, answered, explained and completed.