Question 1172954: For the standard form polynomial f(x)=2x^4-13x^3+2x^2+82x-40 find its roots and write it as the product of linear factors.
Found 3 solutions by ankor@dixie-net.com, greenestamps, ewatrrr:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! For the standard form polynomial

find its roots and write it as the product of linear factors.
Use synthetic division, try x=4
:
.. _______________________
4|2 - 13 + 2 + 82 - 40
. . .+ 8 -20 - 72 + 40
. -----------------------
. 2 - 5 + 18 + 10
Factors are
(x-4)(2x^3 - 5x^2 - 18x + 10)
I don't think you can get more than 1 linear factor is this
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
(previous response replaced -- contained arithmetic errors....)
By the rational roots theorem, the possible rational roots are
(plus or minus) {1, 2, 4, 5, 8, 10, 20, 40; 1/2, 5/2}
You can test each rational root using synthetic division; but that is very tedious.
Finding the roots using a graphing calculator is fast and easy. The factorization is

The quadratic formula gives the roots of the quadratic factor as
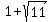 and and 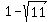
So if you really need to write the polynomial as a product of linear factors, it is
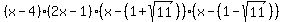
Answer by ewatrrr(24785)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Hi,
f(x)=2x^4-13x^3+2x^2+82x-40
4| 2 -13 2 82 -40
8 -20 -72 40
2 -5 -18 10 0
2x^3 - 5x^2 -18x + 10
1/2| 2 -5 -18 10
1 -2 -10
2 -4 -20 0
2x^2 - 4x - 20
2(x-4)(x-1/2)(x^2 -2x -10)
(x-4)(2x-1)(x^2 -2x -10)
|
|
|