Graph the ellipse and find the coordinates of the center
vertices and foci.
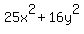= 400
equations of the form 
have their center at the
origin. So the center is (0,0)
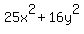= 400
We want to get this either to the form
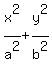= 1 or 
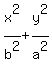= 1
The first one is shaped like an egg sitting on a table.
The second one has the shape of the number zero, like this " 0 ".
We will know which form it is in because 
is always larger
than 
.
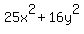= 400
Get 1 on the right by dividing through by 400:
= 
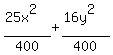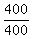
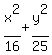= 1
The larger denominator on the left side is 25,
so a² = 25, the smaller denominator of the left
is 16, so b² = 16.
So this graph is in the form 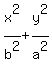= 1
and it will have the shape of a 0.
Since a² = 25, a = 5, Since b² = 16, b = 4
The center is at the origin.
One half the major axis extends from (0,0) to (0,5),
and the other half extends from (0,0) to (0,-5).
One half the minor axis extends from (0,0) to (4,0),
and the other half extends from (0,0) to (-4,0).
So we draw an upright rectangle through those four
points, like this:
Draw an upright ellipse just fitting in that rectangle,
shaped like a zero "0":
It's vetices are the "bluntest" points on the ellipse.
They are (0,5) and (0,-5)
Erase the rectangle:
Now we calculate the value of c which in the distance
from the center to the foci. You can remember what
c is by noticing that the words "focus", "foci", and
"center" contain the letter "c".
The formula is c² = a² - b²
c² = 25 - 16
c² = 9
c = 
c = 3
So the foci are at (0,3) and (0,-3) marked below with
short lines at those points:
Edwin
