|
Question 1172699: How would you factor a polynomial? My equation is
3x^2+4x+1
Thank you!
Found 5 solutions by josgarithmetic, Theo, MathTherapy, greenestamps, ikleyn:
Answer by josgarithmetic(39629)   (Show Source):
You can put this solution on YOUR website! A polynomial could be expected result of two binomial factors.
Look for all the combinations you can think and test them. That's one way.
.
.
Answer by Theo(13342)  (Show Source):
You can put this solution on YOUR website! there are several ways to factor a quadratic equation.
if all else fails, use the quadratic formula.
that formula is:
-b plus or minus sqrt(b^2 - 4ac)
x = -----------------------------------
2a
the quadratic equation has to be placed in the form of:
ax^2 + bx + c = 0
a is the coefficient of the x^2 term
b is the coefficient of the x term
c is the constant.
set your equation equal to 0 and it's already in this form.
you get:
a = 3
b = 4
c = 1
solve for x to get:
x = (-4 plus sqrt(4^2 - 4*3*1)) / 6, or:
x = (-4 minus sqrt(4^2 - 4*3*1)) / 6
since sqrt(4^2 - 4*3*1) is equal to sqrt(4) which is equal to 2, you get:
x = (-4 + 2) / 6, or:
x = (-4 - 2) / 6
this gets you:
x = -1/3 or x = -1
the following graph of the equation shows that this is true.
for quadratic equations, the quadratic formula is the formula that will find the roots, regardless if they are real or not.
there are other ways to factor the quadratic equation as well, but the one method that works every time is the quadratic formula.
the quadratic formula only works on quadratic equations.
if you have a polynomial of a higher degree, you need to use other methods.
there are references on the web that can help you with the various ways to factor a quadratic equations.
here's a selection of some of them.
i did a search on how to solve a quadratic equaton using google.
https://www.google.com/search?q=how+to+solve+a+quadratic+equation&rlz=1C1CHBF_en&oq=how+to+solve+a+quadratic+equation&aqs=chrome..69i57j0l7.3990j0j15&sourceid=chrome&ie=UTF-8
Answer by MathTherapy(10556)  (Show Source):
Answer by greenestamps(13208)  (Show Source):
You can put this solution on YOUR website!
If it is factorable, then it is the product of two linear factors:
where a, b, c, and d are integers.
You want the product to be 3x^2+4x+1
Equating coefficients, that means...
(1) ac=3
(2) bc+ad=4
(3) bd=1
The only way for ac=3 to be a product of two integers is if a and c are 1 and 3.
The only way for bd=1 to be a product of two integers is if b and d are both 1.
That make the only possible factorization
That factorization give us the right coefficient for the middle term: bc+ad = 1(3)+1(1) = 3+1 = 4.
Answer by ikleyn(52873)  (Show Source):
You can put this solution on YOUR website! .
Such problem may perplex an average person.
No, be sure, I know that I can solve a quadratic equation and find the roots,
but the problem is not about solving a quadratic equation.
I know that I can pick up coefficients making trials and errors manipulating with coefficients -
but the problem is not about it.
+-------------------------------------------------------------+
| The problem is about solving it quickly and mentally, |
| without using heavy artillery . . . |
+-------------------------------------------------------------+
OK, then I divide the given polynomial MENTALLY by x^2 and get  +  +  .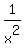
I then replace  by new variable "u" (MENTALLY) and get new polynomial 
with the leading coefficient of 1.
For this polynomial, every person (including me) can guess its factoring in 1-2-3 seconds: it is = (u+1)*(u+3).
Now I take step back making replacement u = MENTALLY.
It gives me factoring of the original polynomial as
3x^2 + 4x + 1 = (x+1)*(3x+1).
and leads to the final answer.
--------------
This description is long (and may seem to be long), but the human's thought runs much faster and gives the answer in seconds.
So, the problem can be solved in this way in 5 seconds MENTALLY, without using paper and pencil or computer.
OK, may be you need to write one line on the paper . . .
The way is simply to convert the given quadratic polynomial into other quadratic polynomial with the leading coefficient of 1.
Then the guessing is 2 seconds and returning back is another 2 seconds - - - and everything can be done in 5 seconds.
|
|
|
| |
