Question 1172688: A grocer mixes chocolates worth 360 pesos per kilo with chocolate worth 400 pesos per
kilo, making a mixture to sell at 372 pesos per kilo. If he mixes 50 kilos total, how many
kilos of each kind does he use?
Found 3 solutions by ikleyn, greenestamps, josgarithmetic:
Answer by ikleyn(52900)   (Show Source):
You can put this solution on YOUR website! .
You may start from this system of 2 equations in two unknowns
x + y = 50 kilograms (mass equation)
360x + 400y = 372*50 pesos. (money equation)
You do the rest.
Or, equivalently, you may start with one single equation
360x + 400*(50-x) = 372*50 (money equation)
and easily solve it
x = 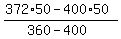 = 35.
ANSWER. 35 kilo at 360 pesos per kilo and (50-35) = 15 kilo at 400 pesos per kilo.
Solved.
Answer by greenestamps(13214)  (Show Source):
You can put this solution on YOUR website!
Here is a quick and easy alternative to the standard algebraic solution method shown by the other tutor.
(1) The price of the mixture per kilo, 372, is 12/40 = 3/10 of the way from 360 to 400, the prices per kilo of the two kinds of chocolates. (Look at the three numbers on a number line, if it helps....)
(2) That means 3/10 of the mixture is the more expensive chocolates.
ANSWER: 3/10 of 50 kilos = 15 kilos of the more expensive chocolates; the other 35 kilos of the less expensive.
CHECK:
15(400)+35(360) = 6000+12600 = 18600
50(372) = 18600
Answer by josgarithmetic(39630)  (Show Source):
|
|
|
