SOLUTION: The earth moves in an elliptic orbit about the sun, with the sun at one focus. The least and greatest distances of the earth from the sun are 147,136,600 kilometers and 152,147,000

Let "a" be the length of the major semi-axis, in kilometers, and

let "e" be the linear eccentricity (the distance from the ellipse center to the the focus).


Then  a + e  is the maximum distance from the focus to the point on the ellipse (from the sun to the orbiting Earth),

and   a - e  is the minimum distance from the focus to the point on the ellipse (from the sun to the orbiting Earth).



Thus we have these two equations


    a + e = 152147000  kilometers    (1)

    a - e = 147136000  kilometers    (2)



By adding the equations, you get

    2a = 152147000 + 147136000 = 299283000,

     a = 299283000/2 = 149641500   kilometers.


Then for the linear eccentricity "e" you get from equation (1)

    e = 152147000 - 149641500 = 2505500 kilometers.


The eccentricity of the ellipse is the ratio 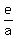  = 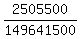 = 0.016743 = 1.6743%.


ANSWER.  The length of the major axis is  2a = 299283000 kilometers.

         the eccentricity is 0.016743.