SOLUTION: Given P(A) = 0.74 , P(B) = 0.25 , and P(A ∩B) = 0.13. Calculate (1) P(A ∪B) (2) P(A ∩B’) (3) P(A’|B’)

(1)  It is easy.

     Use the basic general formula of elementary probability theory

             P(A U B) = P(A) + P(B) - P(A ∩ B) = 0.74 + 0.25 - 0.13 = 0.86.    ANSWER



(2)  To calculate P(A ∩ B’), ask yourself what is the set (A ∩ B’) ?

     This set are those elements of A that do not belong to B.

     In other words,  (A ∩ B’) = A \ (A ∩ B), where the sign  " \ " means subtracting the set (A ∩ B) from A.


     After this notice, it is OBVIOUS that  P(A ∩ B’) = P(A) - P(A ∩ B) = 0.74 - 0.13 = 0.61.    ANSWER



(3)  P(A'|B')  is the conditional probability  P(A' ∩ B’) / P(B').


     To calculate P(A' ∩ B’), ask yourself what is the set (A' ∩ B’) ?

     It is the set of elements that do not belong NEITHER A NOR B.

     In other words, it is the COMPLEMENT of the set (A U B) to the universal set.


     THEREFORE, P(A' ∩ B’) = 1 - P(A U B) = 1 - 0.86 = 0.14,

                             as we just defined the value of P(A U B) = 0.86  in n.(1) above.


     After this notice, it is OBVIOUS that  P(A'|B') = P(A' ∩ B’) / P(B') =  =  =  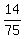= 0.186667 (rounded).    ANSWER