.
Since the coefficients of the polynomial are real numbers (they even are integers (!) ),
it implies that together with the imaginary root 5i, its complex conjugate -5i is also the root.
Hence, the polynimial f(x) is divisible by (x-5i)*(x+5i) = 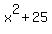 .
When you perform long division, you will get the quotient q(x) =
.
When you perform long division, you will get the quotient q(x) = 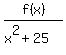 =
= 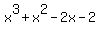 .
You can factor this quotient further using grouping/re-grouping
.
You can factor this quotient further using grouping/re-grouping
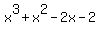 =
= 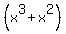 -
- 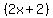 =
= 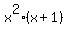 -
- 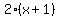 =
= 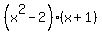 .
Therefore, the full decomposition of the given polynomial over complex number domain is
f(x) =
.
Therefore, the full decomposition of the given polynomial over complex number domain is
f(x) = 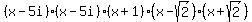 ,
and its roots are 5i, -5i,
,
and its roots are 5i, -5i,  ,
,  and -1. ANSWER
and -1. ANSWER
Solved.