Question 1172444: A lottery offers two 500$ prizes, five 300$ prizes, and ten 100$ prizes. One thousand tickets are sold at 2$ each. Find the expected value if a person buys one ticket.
Found 2 solutions by ikleyn, greenestamps:
Answer by ikleyn(52776)   (Show Source):
You can put this solution on YOUR website! .
The expected win is this amount
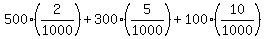 dollars = $3.50.
The expected value is this amount
$3.50 - $2.00 = $1.50.
Statistically, a player has $1.50 in his (or her) pocket in average after each game, if he (or she) plays many times.
Solved, answered and explained.
Answer by greenestamps(13198)  (Show Source):
You can put this solution on YOUR website!
Tutor @ikleyn has provided a response showing how to find the expected value using the formal definition of expected value.
You of course should know the formal definition, and how to calculate the expected value using that definition.
But for many simple expected value problems like this, the answer can be found in a less formal manner.
In this problem, the total cost of the 1000 tickets is $2000, and the total prize payout is $3500. So the payout is $1500 more than the cost of the tickets.
The expected value for one ticket is that $1500, divided by the number of tickets:
$1500/1000 = $1.50
ANSWER: The expected value of one ticket is $1.50.
|
|
|
