SOLUTION: Find the range of the function f(x) = {x^2 + 14x + 9}/{x^2 + 2x + 3}, as x varies over all real numbers. Thanks!

Click here to see ALL problems on Functions

Question 1172442: Find the range of the function
f(x) = {x^2 + 14x + 9}/{x^2 + 2x + 3}, as x varies over all real numbers.
Thanks!
Found 2 solutions by ikleyn, math_tutor2020:
Answer by ikleyn(52784) (Show Source):
You can put this solution on YOUR website!
.

The standard Calculus procedure should be known to you: +--------------------------------------------------------------+ | take a derivative; equate it to zero; find x-coordinate | | of the minimum/maximum, and then calculate the required | | minimum / maximum values. | +----------------------------------------------------------=---+ Notice that the discriminant of the polynomial in the denominator d = b^2 - 4ac = is negative, which means that denominator is zero nowhere in the real numbers domain. Hence, the given rational function is defined everywhere over real numbers and is continuing. It has two horizontal asymptotes as x ---> -oo and/or x ---> oo. So, the function has a maximum and a minimum and does not tend to +/- infinity. Next, to find the minimum/maximum, you can follow the prescription above. But we live in XXI century, so you can use your graphing calculator or other tools from the Internet to facilitate your work. See my plot in the Figure below. Plot y = To find minimum/maximum, I used a special tool from the Internet. The site is https://www.dcode.fr/minimum-function and https://www.dcode.fr/maximum-function It gave me the minimum value of -5 at x = -2 and the maximum value of 4 at x= 1. Thus the range is [-5,4]. ANSWER

Solved.

Answer by math_tutor2020(3817) (Show Source):
You can put this solution on YOUR website!

f(x) = (x^2 + 14x + 9)/(x^2 + 2x + 3)

Let
g(x) = x^2 + 14x + 9
h(x) = x^2 + 2x + 3

Those two other functions are set up such that
f(x) = g(x)/h(x)

This way we can apply the quotient rule
f(x) = g(x)/h(x)
f ' (x) = [ g'(x)*h(x) - g(x)*h'(x) ]/[ (h(x))^2 ]

Let's compute each derivative piece
g(x) = x^2 + 14x + 9
g'(x) = 2x + 14
and
h(x) = x^2 + 2x + 3
h'(x) = 2x + 2

Allowing us to get
f ' (x) = [ g'(x)*h(x) - g(x)*h'(x) ]/[ (h(x))^2 ]
f ' (x) = [ (2x+14)*(x^2+2x+3) - (x^2+14x+9)*(2x+2) ]/[ (x^2+2x+3)^2 ]
f ' (x) = [ 2x^3+18x^2+34x+42 - (2x^3+30x^2+46x+18) ]/[ (x^2+2x+3)^2 ]
f ' (x) = [ -12x^2 - 12x + 24 ]/[ (x^2+2x+3)^2 ]

Solve the derivative equal to 0 to solve for x
Since the denominator cannot be zero, this means the numerator must be 0

f ' (x) = 0
[ -12x^2 - 12x + 24 ]/[ (x^2+2x+3)^2 ] = 0
-12x^2 - 12x + 24 = 0

Apply the quadratic formula to find the roots are
x = -2 and x = 1
I'll skip showing these steps

Now set up a sign chart. Draw a number line. Plot -2 and 1 on the number line. Mark the points as A and B.

We'll need to test three regions:
1) The region to the left of A
2) The region between A and B
3) The region to the right of B
by "test", I mean determine the sign of f ' (x) for these regions. As you can probably guess by now, I'm going to use the first derivative test.
The second derivative test is an alternative option, but it requires calculating the second derivative which is going to be a bit of a pain.

Let's just stick with the first derivative test.

Focus on the region to the left of point A, ie the region to the left of x = -2.

The value x = -3 is one possible test value. Plug this into f ' (x)
f ' (x) = [ -12x^2 - 12x + 24 ]/[ (x^2+2x+3)^2 ]
f ' (-3) = [ -12(-3)^2 - 12(-3) + 24 ]/[ ((-3)^2+2(-3)+3)^2 ]
f ' (-3) = -1.33
Which is approximate.
The actual value doesn't matter. All we're after is whether f ' (x) is positive or negative.
Since f ' (x) is negative, this means f(x) is decreasing on the interval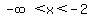

Now test the region between A and B, so the region between x = -2 and x = 1. The value x = 0 is a good candidate.
f ' (x) = [ -12x^2 - 12x + 24 ]/[ (x^2+2x+3)^2 ]
f ' (0) = [ -12(0)^2 - 12(0) + 24 ]/[ ((0)^2+2(0)+3)^2 ]
f ' (0) = 2.667
Also approximate.
The result here is positive.
So f(x) is increasing on the interval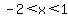

The change from decreasing to increasing through indicates we have a local minimum here. Check out the graph below and it visually confirms this.

The last region to check is everything to the right of B, so when x > 1
I'll pick x = 2
f ' (x) = [ -12x^2 - 12x + 24 ]/[ (x^2+2x+3)^2 ]
f ' (2) = [ -12(2)^2 - 12(2) + 24 ]/[ ((2)^2+2(2)+3)^2 ]
f ' (2) = -0.397
Approximately.
We get a negative value.
f(x) is decreasing on the interval
The change from increasing (previous interval) to decreasing shows we have a local max.

To summarize:
x = -2 leads to a local min
x = 1 leads to a local max

Plug each of these values into the original f(x) function to find the actual local min and local max

Local Min:
f(x) = (x^2 + 14x + 9)/(x^2 + 2x + 3)
f(-2) = ((-2)^2 + 14(-2) + 9)/((-2)^2 + 2(-2) + 3)
f(-2) = -5
The lowest f(x) can go is f(x) = -5. We can say where y = f(x)

Local Max:
f(x) = (x^2 + 14x + 9)/(x^2 + 2x + 3)
f(1) = ((1)^2 + 14(1) + 9)/((1)^2 + 2(1) + 3)
f(1) = 4
The highest f(x) can go is f(x) = 4. We can say

Combine with , ie overlap the two intervals (use a number line if needed), and we get which represents the range

In short, the range is any real number between -5 and 4, including both endpoints.

The graph below visually confirms this

Side note: The horizontal asymptote is y = 1, which can be determined through applying a limit as x goes to either infinity.

------------------------------------------

Answer: Range is