Looking at base = e, and ln (the natural log)...
A graph showing  ,
,  , and
, and  is a quick way to see they will never intersect.
is a quick way to see they will never intersect.
Aside from that... for 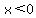 , clearly
, clearly 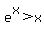 as
as 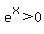 while
while  . For the half-plane x>=0, one can write the Taylor series expansion for
. For the half-plane x>=0, one can write the Taylor series expansion for  :
:
 =
= 
Pull out the first two terms from the RHS:
 =
= 
So clearly 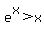 for
for  and combined with the first part,
and combined with the first part, 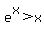 for all x.
for all x.
To prove 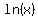 <
< 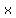 (here the domain of x is x>0, as ln(x) is not defined for
(here the domain of x is x>0, as ln(x) is not defined for  ), we can use the result from above as the starting point:
), we can use the result from above as the starting point:
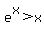
Take ln() both sides:
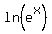 >
> 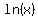
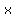 >
> 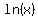 , x>0
, x>0