Question 1172391: If z.x^2 - 2.y.z^2 + x.y = 0 then find partial derivative of x w.r.t z at point (1, 1, 1)? [Here ^2 means power 2]
Found 2 solutions by ewatrrr, ikleyn:
Answer by ewatrrr(24785)   (Show Source):
Answer by ikleyn(52911)  (Show Source):
You can put this solution on YOUR website! .
If z.x^2 - 2.y.z^2 + x.y = 0 then find partial derivative of x w.r.t z at point (1, 1, 1)?
~~~~~~~~~~~~~~~
Although it was not pronounced in the problem's formulation, from the context we should consider
z as the independent variable, and x = x(z) and y = y(z) as the functions of the independent variable z.
By default, it is the ONLY ONE UNIQUE correct way to interpret the condition, and
(by default, again) there is NO OTHER way to interpret it.
+-----------------------------------------------------------------------------------------------------------+
| I will not repeat that obvious fact that if the problem (or its composer) means something different, |
| then this different must be explicitly and directly pointed in the condition. |
+-----------------------------------------------------------------------------------------------------------+
Therefore, we should apply the rule of differentiating products everythere (to each and every term) properly and consistently.
By doing this way, we will get (in what follows, I use x' =  and y' = 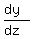 as shortcuts)
2z*x*x' - (2y'*z^2 + 2y*2z) + x'*y + x*y' = 0
2z*x*x' + x'*y = 2y'*z^2 + 4yz - x*y'
x' = (2y'*z^2 + 4yz - x*y') / (2zx + y).
Now you can substitute the given values x= 1, y= 1 and z= 1
x' = (2y' + 4 - y')/3 = (y' + 4)/3.
It is the answer. Since y'(1) is not given in the condition, we can not move further.
If y is not a function of z (in other words, if y is considered as a constant function of z),
then in the last formula we should put y' = 0.
We will get then x' = 4/3.
|
|
|
