.
If function f = u + iv is analytic when u = Sin(x).Cosh(y) then what is the  expression of v?
expression of v?
~~~~~~~~~~~~~~~~~~~
If the complex-value function f = u + iv is analytic, then the Cauchy-Riemann equations are held
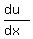 =
= 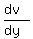 (1)
and
(1)
and
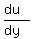 = -
= - 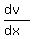 (2)
(as the reference, see this Wikipedia article https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations ).
I am very sorry, but in these equations the symbol "d" must be a Greek letter ("d rounded"), not a "d" Latin,
but in this editor I can not reproduce it, unfortunately. So, concider this "d" as "d rounded" in all my
formulas in this post).
From equation (1), after differentiating
(2)
(as the reference, see this Wikipedia article https://en.wikipedia.org/wiki/Cauchy%E2%80%93Riemann_equations ).
I am very sorry, but in these equations the symbol "d" must be a Greek letter ("d rounded"), not a "d" Latin,
but in this editor I can not reproduce it, unfortunately. So, concider this "d" as "d rounded" in all my
formulas in this post).
From equation (1), after differentiating 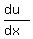 , we have
, we have
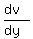 = cos(x)*cosh(y) (3)
From equation (2), after differentiating
= cos(x)*cosh(y) (3)
From equation (2), after differentiating 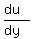 , we have
, we have
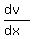 = -sin(x)*sinh(y) (4)
So, we need to find function v as antiderivative from equations (3) and (4).
It is easy to do: the function v(x,y) = cos(x)*sinh(y) satisfies both equations (3) and (4).
THEREFORE, the answer to the problem's question is v = cos(x)*sinh(y).
= -sin(x)*sinh(y) (4)
So, we need to find function v as antiderivative from equations (3) and (4).
It is easy to do: the function v(x,y) = cos(x)*sinh(y) satisfies both equations (3) and (4).
THEREFORE, the answer to the problem's question is v = cos(x)*sinh(y).
Solved.
You may add an arbitrary constant value to "v" to provide "a general view" to satisfy your professor :).