.
It is well known, obvious and self-evident fact that every degree 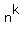 gives the remainder 1, when is divided by (n-1).
Therefore, the sum n + 2n^2 + 3n^3 + . . . + 2019n^2019 gives the remainder
1 + 2 + 3 + . . . + 2019
when is divided by (n-1).
In turn, the sum 1 + 2 + 3 + . . . + 2019 is the sum of the first 2019 natural numbers, and, therefore, is equal to
gives the remainder 1, when is divided by (n-1).
Therefore, the sum n + 2n^2 + 3n^3 + . . . + 2019n^2019 gives the remainder
1 + 2 + 3 + . . . + 2019
when is divided by (n-1).
In turn, the sum 1 + 2 + 3 + . . . + 2019 is the sum of the first 2019 natural numbers, and, therefore, is equal to
 =
=  = 1010*2019.
The number 1010*2019 has THIS DECOMPOSITION into the product of prime numbers
1010*2019 = (2*5*101)*(3*673).
So, its decomposition is the product of 5 prime numbers with multiplicities 1 for each participating prime.
Therefore, the number of divisors of the number 1 + 2 + 3 + . . . 2019 = 1010*2019 is
(1+1)*(1+1)*(1+1)*(1+1)*1+1) = 2*2*2*2*2 =
= 1010*2019.
The number 1010*2019 has THIS DECOMPOSITION into the product of prime numbers
1010*2019 = (2*5*101)*(3*673).
So, its decomposition is the product of 5 prime numbers with multiplicities 1 for each participating prime.
Therefore, the number of divisors of the number 1 + 2 + 3 + . . . 2019 = 1010*2019 is
(1+1)*(1+1)*(1+1)*(1+1)*1+1) = 2*2*2*2*2 =  = 32.
Each such divisor is the potential number (n-1).
THEREFORE, the answer to the problem's question is 32.
= 32.
Each such divisor is the potential number (n-1).
THEREFORE, the answer to the problem's question is 32.
Solved.