Question 1172151: 1.If r and s are the roots of the quadratic equation x2 + 3x - 5 = 0, find the value of r3 + s3. Show clear solution pls thanksss!
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
We can use Vieta's Formulas to say
r+s = -b
r*s = c
where r,s are the two roots of x^2+bx+c
In this case, a = 1.
If 'a' was some nonzero value other than 1, then you'd have to divide everything by 'a' to get ax^2+bx+c into the form x^2+px+q, where p = b/a and q = c/a.
From x^2+3x-5, we see that b = 3 and c = -5
Plug those values into the first two equations mentioned to get:
r+s = -3
r*s = -5
Let's square both sides of that first equation and do a bit of rearranging:
r+s = -3
(r+s)^2 = (-3)^2
r^2+2rs+s^2 = 9
r^2+s^2+2rs = 9
r^2+s^2+2(-5) = 9 ... plug in rs = -5
r^2+s^2-10 = 9
r^2+s^2 = 9+10
r^2+s^2 = 19
The following three equations
r+s = -3
r*s = -5
r^2+s^2 = 19
will be used in the next portion below
By the sum of cubes factoring formula, we know that...
r^3+s^3 = (r+s)(r^2-rs+s^2)
r^3+s^3 = (r+s)(r^2+s^2-rs)
r^3+s^3 = (-3)(r^2+s^2-rs) ... plug in r+s = -3
r^3+s^3 = (-3)(19-rs) .... plug in r^2+s^2 = 19
r^3+s^3 = (-3)(19-(-5)) .... plug in rs = -5
r^3+s^3 = (-3)(19+5)
r^3+s^3 = (-3)(24)
r^3+s^3 = -72 which is the final answer.
-------------------------------------------------------
As you can see from the last section, we computed r^3+s^3 without knowing what r and s are individually. We could actually solve for them using the quadratic formula
I won't show those steps, but you should get 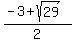 and and  as the two roots. as the two roots.
These are the values of r and s in either order.
Once you know these values, plug them into r^3+s^3 and you should get -72 as the final answer.
Also, knowing the actual roots r,s allows you to check each of these following equations
r+s = -3
r*s = -5
r^2+s^2 = 19
to help further confirm the steps of the previous section. I'll let you perform these checks.
-------------------------------------------------------
Answer: -72
Answer by ikleyn(52803)   (Show Source): (Show Source):
|
|
|