SOLUTION: Find the values of Arcsin 2x in the equation : Arcsin 2x - Arcsin x =pi/3

Algebra ->  Rate-of-work-word-problems -> SOLUTION: Find the values of Arcsin 2x in the equation : Arcsin 2x - Arcsin x =pi/3       Log On


   

Question 1172108: Find the values of Arcsin 2x in the equation :
Arcsin 2x - Arcsin x =pi/3
Found 2 solutions by math_tutor2020, ikleyn:
Answer by math_tutor2020(3817) About Me  (Show Source):
You can put this solution on YOUR website!

Hint:

You'll use very similar steps found here
https://socratic.org/questions/how-do-you-solve-arcsin-x-arcsin-2x-pi-3
Though instead of alpha%2Bbeta+=+pi%2F3, you are considering alpha-beta+=+pi%2F3, where alpha+=+arcsin%282x%29 and beta+=+arcsin%28x%29

Caution: The link posted has an error in one of the steps. Specifically the step where it says this

The -4x%5E4 should be %22%22%2B4x%5E4 since %28-x%5E2%29%2A%28-4x%5E2%29+=+4x%5E4. Once this error is corrected, it will lead to the correct answer for alpha%2Bbeta+=+pi%2F3. Keep this in mind when you apply your steps to get the answer you're after.

Answer by ikleyn(52803) About Me  (Show Source):
You can put this solution on YOUR website!
.
Find the values of Arcsin 2x in the equation :
Arcsin 2x - Arcsin x = pi/3
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ 


Let  "a"  be the angle  - pi%2F2 <= a <= pi%2F2,  sin(a) = x,  and 

Let  "b"  be the angle  - pi%2F2 <= b <= pi%2F2,  sin(b) = 2x.


They want you find the value of x such that

    b - a = pi%2F3.      (1)


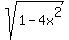Since sin(a) = x  and  sin(b) = 2x,  we have  cos(a) = sqrt%281-x%5E2%29,  cos(b) = sqrt%281-4x%5E2%29.


From equation (1), taking cosine from both sides, we have this equation

    cos(b-a) = cos%28pi%2F3%29,                  or

    cos(b)*cos(a) + sin(b)*sin(a) = 1%2F2,   or, substituting

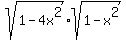    sqrt%281-4x%5E2%29%2Asqrt%281-x%5E2%29 + (2x)*x = 1%2F2,     or

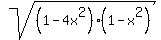    sqrt%28%281-4x%5E2%29%2A%281-x%5E2%29%29 = 1%2F2 - 2x^2.


Now square both sides.  You will get then

    (1-4x^2)*(1-x^2) = 1%2F4 - 2x^2 + 4x^4.


Simplify it step by step

    1 - 4x^2 - x^2 + 4x^4 = 1%2F4 - 2x^2 + 4x^4

    1 - 5x^2              = 1%2F4 - 2x^2

    4 - 20x^2             = 1 - 8x^2

    4 - 1                 = 20x^2 - 8x^2

      3                   = 12x^2

      1                   = 4x^2

      x^2                 = 1%2F4

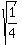      x                   = sqrt%281%2F4%29%29 = +/- 1%2F2.


Thus the equation is just solved,  and we have two potential solutions  x= +/- 1%2F2.


    Consider these two cases separately and check the results in both cases.



Case a).  x = 1%2F2;  arcsin(x) = pi%2F6;  2x = 1;  arcsin(2x) = arcsin(1) = pi%2F2.

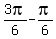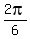          Since  pi%2F2 - pi%2F6 = 3pi%2F6+-+pi%2F6 = 2pi%2F6 = pi%2F3,  the solution is correct.



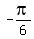Case b).  x = - 1%2F2;  arcsin(x) = - pi%2F6;  2x = -1;  arcsin(2x) = arcsin(-1) = - pi%2F2.

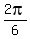          Since  -pi%2F2 - -pi%2F6 = -3pi%2F6+%2B+pi%2F6 = - 2pi%2F6 = - pi%2F3,  this solution DOES NOT work. It is EXTRANEOUS.


   +--------------------------------------------------------------------+
   |  So, the problem has a unique solution                             |
   |                                                                    |
   |  x = 1%2F2,  and  arcsin(x) = pi%2F6,  arcsin(2x) = pi%2F2.                 | 
   +--------------------------------------------------------------------+


Solved.


/\/\/\/\/\/\/\/

Post-solution notes: 

1)  The solution under the link

    https://socratic.org/questions/how-do-you-solve-arcsin-x-arcsin-2x-pi-3

    mentioned by tutor  @Math_tutor2020, is INCORRECT.



2)  The solution by @Math_tutor2020 also contains a technical error.

    It is WHY I came to bring the correct and accurate solution.