SOLUTION: A bakery has created a new type of donut that is driving the competition out of the market. They are currently selling the donuts for $3 each and sell 1400 donuts each month. Mark

Let n be the number of increments by $0.25.


Then the price for each donut is p(n) = 3 + 0.25n and the number of the sold donutes is  1400-70n.


Hence, the revenue is

    R(n) = p(n)*(1400 - 70n) = (3 + 0.25n)*(1400 - 70n).


It is a quadratic function , presented as the product of the two linear binomial.

The quadratic function has the roots there, where the linear binomials are zer0, i.e. at

      n = -12  and  n= 20.


The maximum of the quadratic function is achieved at the midpoint between its roots, i.e. at 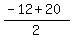  = 4.


So, 4 (four) increases at $0.25 each are required to get the maximum revenue.


Thus the optimum price per donut is  3 + 4*0.25 = 4 dollars.

The optimum sale is then  1400 - 4*70 = 1120 donuts, and the maximum revenue is

    4*1120 = 4480 dollars.


Compare it with the starting revenue of  3*1400 = 4200 dollars.