|
Question 1171978: The Electrocomp Corporation manufactures two electrical products: air conditioners and large fans. The assembly process for each is similar in that both require a certain amount of wiring and drilling. Each air conditioner takes 6 hours of wiring and 1 hours of drilling. Each fan must go through 2 hours of wiring and 1 hours of drilling. During the next production period, 240 hours of wiring time are available and up to 77 hours of drilling time may be used. Each air conditioner sold yields a profit of $20. Each fan assembles may be sold for a $15 profit. Formulate and solve this LP production mix situation to find the best combination of air conditioners and fans that yields the highest profit. Use the corner point graph approach
Found 2 solutions by Theo, ikleyn:
Answer by Theo(13342)   (Show Source):
You can put this solution on YOUR website! set up a table as shown beloow:
x y
air conditioner fan
wiring 6 1 <= 240
drilling 2 1 <= 77
profit 25 15 maximize
your objective function is 25x + 15y.
this is what you want to maximize.
your constraint functions are:
6x + y <= 240
2x + y <= 77
x >= 0
y >= 0
using the desmos.com calculator, you will graph the opposite of the contsraint functions.
the area on the graph that is not shaded is your region of feasibiliy.
your maximum profit will be at the corner points of the feasible region.
you find the maximum profit by evaluating the objective function at each of the corner points.
the graph looks like this.
total profit is shown below with all constraints met.
x y drill wire profit
0 77 154 77 1155
21.5 55.5 240 77 1370
40 0 240 40 1000
total drill hours are less than or equal to 240
total wire hours are less than or equal to 77
maximum total profit is 1370 when x = 21.5 and y = 55.5
Answer by ikleyn(52798)  (Show Source):
You can put this solution on YOUR website! .
The Electrocomp Corporation manufactures two electrical products: air conditioners and large fans.
The assembly process for each is similar in that both require a certain amount of wiring and drilling.
Each air conditioner takes 6 hours of wiring and 1 hour of drilling.
Each fan must go through 2 hours of wiring and 1 hour of drilling.
During the next production period, 240 hours of wiring time are available and up to 77 hours of drilling time may be used.
Each air conditioner sold yields a profit of $20. Each fan assembles may be sold for a $15 profit.
Formulate and solve this LP production mix situation to find the best combination of air conditioners and fans
that yields the highest profit. Use the corner point graph approach
~~~~~~~~~~~~~~~
The solution by @Theo contains several technical errors and one conceptual error,
which leads to nonsensical answer in non-integer numbers
21.5 air conditioners and 55.5 large fans.
Therefore, I came to bring a correct solution.
Let x be the number of air conditioners and let y be the number of fans.
Then the objective function to maximize is the profit
P(x,y) = 20x + 15y dollars.
The constraints are
6x + 2y <= 240 (hours of wiring)
x + y <= 77 (hours of drilling)
x >= 0, y >= 0.
The constraints form THIS feasibility domain in the first quadrant QI, shown in the Figure below:
Plot y = 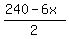 (red line) and y = 77-x (green line)
Feasibility domain is a quadrilateral in QI below both red and green lines adjacent to coordinate axes.
Feasibility domain has 3 vertices:
P1 = (0,77) (y-intercept to green line);
P2 = (21.5,55.5) (intersection point of the red and green line);
P3 = (40,0) (x-intercept to red line).
You should calculate the value of the objective function P(x,y) = 20x + 15y at these three points:
at P1: P(x,y) = 20*0 + 15*77 = 1155;
at P2: P(x,y) = 20*21.5 + 15*55.5 = 1262.5;
at P3: P(x,y) = 20*40 + 15*0 = 800.
Comparing the values, you see that the maximum is achieved at the point P2 = (21.5,55.5), where x= 21.5, y= 55.5, and is equal to 1262.5.
But STOP for a minute (!)
This answer MAKES no SENSE, since we get the "solution" in non-integer numbers.
Why we got an absurdist solution ? - Because we, actually, missed one important constraint at the setup step:
The final answer must be in integer numbers.
So, this problem is not a simplest traditional Linear Programming problem.
It is, actually, an integer Linear Programming problem, which means that the solution should be found among integer numbers.
Unfortunately, the naive simplest algorithm, which works and traditionally is used for LP-problems,
DOES NOT work for integer LP-problems.
Which is even worst, I could not find in the Internet free of charge robust online solver for such integer LP-problems.
Nevertheless, there is the way to complete the solution even in these non-favorable circumstances.
The way is to trace all appropriate candidate integer points (x,y) in the coordinate plane; calculate the Profit function in all these points
and select then the point with the maximum profit among them.
It can be done using Excel, as I describe it below.
In Excel, I formed a spreadsheet (see below).
The first column lists integer x-coordinates from 1 to 40.
The next column lists integer values of y = 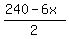= 120 - 3x for x = 1, 2, 3, . . . , 21.
The third column lists integer values of y = 77 - x for x = 22, 23, 24, . . . , 40.
The last column is the profit function, calculated for these x- and y- integer values.
x y = 77-x y = 120-3x P = 20x+15y
1 76 1160
2 75 1165
3 74 1170
4 73 1175
5 72 1180
6 71 1185
7 70 1190
8 69 1195
9 68 1200
10 67 1205
11 66 1210
12 65 1215
13 64 1220
14 63 1225
15 62 1230
16 61 1235
17 60 1240
18 59 1245
19 58 1250
20 57 1255
21 56 1260 <<<---===
22 54 1250
23 51 1225
24 48 1200
25 45 1175
26 42 1150
27 39 1125
28 36 1100
29 33 1075
30 30 1050
31 27 1025
32 24 1000
33 21 975
34 18 950
35 15 925
36 12 900
37 9 875
38 6 850
39 3 825
40 0 800
The maximum profit is 1260 dollars; it corresponds to the values of x= 21 and y= 56.
Thus the problem is just solved, and the answer is: 21 air conditioner and 56 large fans provide the maximum profit of 1260 dollars.
Solved.
|
|
|
| |
