Question 1171970: An electronics firm is planning to market a new graphing calculator. The fixed costs are $100,000
and the variable costs are $47 per calculator. The wholesale price of the calculator will be $63. If
x is the number of calculators, then the revenue is given by 𝑅 = 63𝑥 and the cost is given by
𝐶 = 47𝑥 + 100,000.
(A) For the company to make a profit, it is clear that revenues must be greater than
costs. How many calculators must be sold for the company to make a profit? [2pts]
(B) The profit is determined by revenue minus cost. How many calculators were sold if
the profit is more than $250,000 but less than $300,000? [5pts]
Answer by Theo(13342)   (Show Source): (Show Source):
You can put this solution on YOUR website! revenue function is r = 63 * x
cost function is c = 47 * x + 100,000
profit is equal to revenue minus cost.
let p = profit to get:
p = 63 * x - 47 * x - 100,000
simplify to get:
p = 16 * x - 100,000
to make a profit, p must be > 0
this means that 16 * x - 100,000 > 0.
your inequality to solve is 16 * x - 100,000 > 0
add 100,000 to both sides of this inequality to get:
16 * x > 100,000
solve for x o get:
x > 100,000 / 16
result is x > 6230
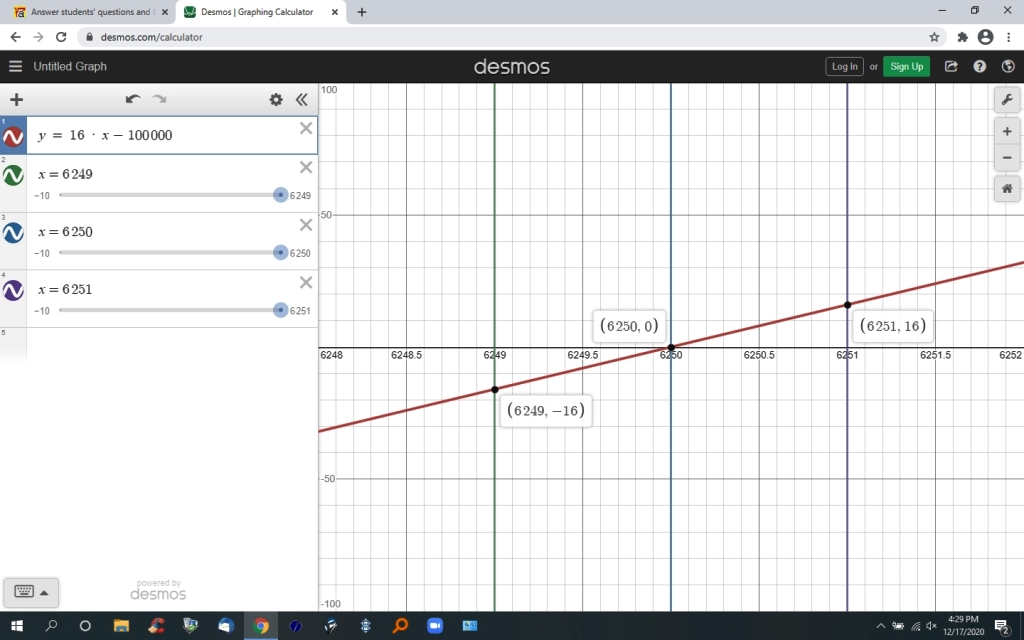
wh3en x = 6249, 16 * x - 100,000 = -16
a profit of -16 means a loss of 16.
when x = 6250, 16 * x - 100,000 = 0
a profit of 0 means no profit and no loss, i.e. you broke even.
when x = 6251, 16 * x - 100,000 = 16
profit starts being made when more than 6250 calculators are sold.\
on a graph, this looks like this.
|
|
|