SOLUTION: Find the reference angle for θ= -22pi/9 ​

The radian measure for 0°, 90°, 180°, 270°, and 360° are

0, π/2, π, 3π/2, and 2π which have approximate decimal values:

0, 1.57, 3.14, 2.36, and 6.28. 

We can add any integer, positive or negative times  and
have an angle coterminal with .

First we find the smallest coterminal angle which is between 0 and 2π,



Clear of fractions by multiplying through by 9



Divide all three sides by 2π



Add 11 to all three sides:



Divide through by 9





Since n must be an integer,



Substitute n=2 in 











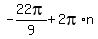
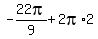
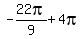
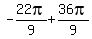
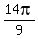This is approximately 4.89 which puts it in QIV

So to get the reference angle, we subtract from 2π:





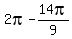
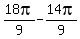
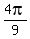  <-- reference angle.

Edwin