|
Question 1171787: Gabo can do a job in one hour less then Wynter. If Gabo and Wynter work together the job takes 6/5 hours.How long would it take each person working alone?
Found 2 solutions by josgarithmetic, ikleyn:
Answer by josgarithmetic(39631)   (Show Source):
Answer by ikleyn(52925)  (Show Source):
You can put this solution on YOUR website! .
In his post, @josgarithmetic offers you to solve this equation  .
This equation is INCORRECT, so you better IGNORE it, for your safety :  .
The correct equation is
 +  =  ,
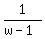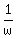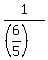or, equivalently,
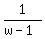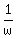+ =  . (1)
At this point a person familiar with arithmetic operations on fractions just can to guess the solution
w= 3, since  +  = .
But if you want to have full formal algebraic solution, let's do it step by step.
Multiply equation (1) by 6w*(w-1) (both sides). You will get then
6w + 6*(w-1) = 5w*(w-1)
6w + 6w - 6 = 5w^2 - 5w
5w^2 - 17w + 7 = 0
(w-3)*(5w+2) = 0.
It has two roots, one positive and one negative.
Only positive root w= 3 is the solution to the problem,
confirming that my earlier guess was correct.
ANSWER. Winter makes the job in 3 hours; Gabo makes it in 2 hours.
----------------
To see other similar solved problems, look into the lesson
- Using quadratic equations to solve word problems on joint work
in this site.
Learn the subject from there.
Happy learning (!)
/\/\/\/\/\/\/\/
After my notice, @josgarithmetic changed his post.
|
|
|
| |
