Question 1171755: Sam is at the origin in the coordinate plane. Every minute, he flips a coin. If he gets
heads, he walks right one unit. Otherwise, he walks left one unit. After five minutes,
what is the probability is at (1,0)?
Found 2 solutions by Solver92311, ikleyn:
Answer by Solver92311(821)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The answer depends on whether he flipped the coin at time zero and every minute thereafter for five minutes (a total of six flips) or if he waited until minute 1 to flip the coin the first time (a total of 5 flips).
If it is the first condition, the probability of landing on (1,0) or any point with an odd abscissa is zero because if you have an even number of coin flips, you must land on an even abscissa, i.e, (-6,0), (-4,0), ... (0,0), ... (4,0), (6,0).
If five flips you have to get three heads and two tails. So the probability is the number of ways that you can get three heads and two tails divided by the number of results possible when flipping 5 coins.
The number of ways to get  heads in heads in  coin flips is given by coin flips is given by !}) and the number of possible outcomes with and the number of possible outcomes with  coin flips is coin flips is  . Happy arithmetic. . Happy arithmetic.
John

My calculator said it, I believe it, that settles it

From
I > Ø

Answer by ikleyn(52879)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
The meaning / (the context) of this problem is that Sam flips the coin at the beginning of each minute t= 0, 1, 2, 3, 4,
and, depending on the result of each individual flipping, he is 1 unit to the left or 1 unit to the right
from his previous/(current) position on the straight line at the end of THIS minute.
Let H be the number of Heads in 5 flips.
Then the number of Tails is (5-H), and we are interested to find the value of H under this condition
H - (5-H) = 1.
From the equation,
H - 5 + H = 1, 2H = 1 + 5 = 6, H = 6/2 = 3.
Thus, to get the point 1 unit to the right from the beginning after 5 flips, he should have 3 Heads and 2 Tails in his experiment.
What concretely is the sequence of heads and tails in the experiment, it DOES NOT matter.
What does really matter, is to have 3 Heads and 2 Tails in any order of 5 flips.
So, it is a binomial distribution problem with the number of trials n= 5 and the number of success k= 3;
the probability of the success is  = 0.5 in each individual trial.
THEREFORE, the probability under the problem's question is P = = 0.5 in each individual trial.
THEREFORE, the probability under the problem's question is P =  = = 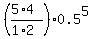 = 0.3125. ANSWER = 0.3125. ANSWER
Solved.
------------
It is a good entertainment problem.
By the way, with 6 flips the probability to get the point (1,0) is equal to ZERO,
because the equation H - (6-H) = 1 DOES NOT have solutions in integer numbers in this case.
|
|
|