Question 1171731: Question: In a set of four numbers, the first three are in a geometric sequence and the last three are in an arithmetic sequence with a common difference of 6. If the first number is the same as the fourth, find the four numbers.
What I have come up with so far:
GP: a, ar, ar^2
AP ar, ar+6, ar+12
a = ar + 12
ar^2 = ar + 6
I am stuck
Not able to generate a system of equations to solve for a or r.
Please help.
Thanks
Answer by ikleyn(52879)   (Show Source):
You can put this solution on YOUR website! .
n 1 2 3 4
GP a ar ar^2
AP ar ar+6 ar+12
First equation
"the first number is the same as the fourth" : a = ar + 12
Second equation :
the terms under n= 3 in the table are equal : ar^2 = ar + 6.
The system of equations is
a = ar + 12 (1)
ar^2 = ar + 6 (2)
To solve the system, write equations (1) and (2) in equivalent form
a - ar = 12 (1')
ar - ar^2 = -6 (2')
Transform equation (2') to the form r*(a-ar) = -6 and replace (a-ar) in it by 12, based on (1').
You will get then
12r = -6, which implies r = 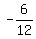 =  = -0.5.
Having it, substitute r = 0.5 into equation (1'). You will get then
a - (-0.5)a = 12
a + 0.5a = 12
1.5a = 12
a = 12/1.5 = 8.
So, a = 8, r = -0.5,
Knowing it, you can calculate all the terms in both progressions.
Solved, answered, explained and completed.
|
|
|
