SOLUTION: You have two planes that need refueling. One plane that can carry fuel has a hose that is 160 feet long. The angle of elevation between the plane being refueled and the hose is 3

Algebra ->  Trigonometry-basics -> SOLUTION: You have two planes that need refueling. One plane that can carry fuel has a hose that is 160 feet long. The angle of elevation between the plane being refueled and the hose is 3      Log On


   

Question 1171659: You have two planes that need refueling.
One plane that can carry fuel has a hose that is 160 feet long. The angle of elevation between the plane being refueled and the hose is 32 degrees. Find the difference in altitudes that is required in order for the plane to refuel.
The other plane that can refuel has a hose that is 140 feet long. The smallest acceptable altitude difference between two planes is 100 feet. What angle should be created in order for the second plane to refuel another plane at that altitude difference?
must include
diagrams representing the two refueling situations along with the calculations that you used to determine the distances and angles
a clear description of the solution that could easily be translated to the pilots
Answer by ikleyn(52848) About Me  (Show Source):
You can put this solution on YOUR website!
.

First question is about the leg of the right-angled triangle opposite to the given angle; the hypotenuse is given.


    So, use the sine  

        difference of altitudes = 160*sin(32°).    (1)




In the second question,  you are given the hypotenuse and the altitude difference.


    Again, you use the same formula, but in other form

        sin(a) = 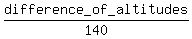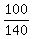difference_of_altitudes%2F140 = 100%2F140 = 0.714.



    So, now find the critical angles as arcsin(0.714).