Question 1171616: Paddlewheel Pat has a motorboat. He can travel a distance of 10 miles boating into the current in the same time it takes him to travel 15 miles with the current. If the current has a speed of 3 mph, what is the speed of Pat’s boat in still water?
Found 2 solutions by ankor@dixie-net.com, greenestamps:
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Paddlewheel Pat has a motorboat.
He can travel a distance of 10 miles boating into the current in the same time it takes him to travel 15 miles with the current.
If the current has a speed of 3 mph, what is the speed of Pat’s boat in still water?
:
let s = his speed in still water
then
(s+3) = his speed with the current
and
(s-3) = his speed against
:
Write a time equation, time = dist/speed
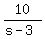 = = 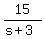
cross multiply
15(s-3) = 10(s+3)
15s - 45 = 10x + 30
15s - 10s = 30 + 45
5s = 75
s = 75/5
s = 15 mph in still water
:
:
Check this by finding the time of each way, should be equal
15/18 = .833 hrs
10/12 = .833 hrs
Answer by greenestamps(13206)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Here is a highly unusual way for solving this kind of problem that I personally find easy to use.
Take a look at it and see if it "works" for you. If not, there are of course many other ways to solve the problem.
The times are the same, and the distances are in the ratio 10:15 = 2:3. That means the speeds are in the ratio 2:3.
If the speed of the boat in still water is x, then the upstream speed is x-3 and the downstream speed is x+3.
Solve for x by writing the ratio 2:3 as an equivalent ratio in which the difference between the two numbers is the difference between the upstream and downstream speeds:

On the left, the difference between numerator and denominator is 1; on the right is is 6. To get the desired equivalent ratio, multiply numerator and denominator on the left by 6.

So x-3 is 12 and x+3 is 18; that means x is 15.
ANSWER: The speed of the boat in still water is 15 mph.
|
|
|