Question 1171585: The complex numbers z and w satisfy |z| = |w| = 1 and zw is not equal to -1.
(a) Prove that \overline{z} = {1}/{z} and \overline{w} = {1}/{w}.
(b) Prove that {z + w}/{zw + 1} is a real number.
Can you please explain in detail? I'm super confused, can someone please help? Thank you so much.
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Part (a)
Let
z = a+bi
w = c+di
where a,b,c,d are real numbers and i = sqrt(-1) or i^2 = -1
Since |z| = 1, this means
|z| = sqrt(a^2+b^2)
1 = sqrt(a^2+b^2)
1^2 = (sqrt(a^2+b^2))^2
1 = a^2 + b^2
a^2 + b^2 = 1
Through similar algebraic steps, we can say,
|w| = 1
leads to
c^2 + d^2 = 1
---------------------------------
Using our definition of z, let's find 1/z


 This step is done to turn the denominator into a real number. This step is done to turn the denominator into a real number.

 Difference of squares rule Difference of squares rule

 Plug in i^2 = -1 Plug in i^2 = -1

 Plug in a^2+b^2 = 1 Plug in a^2+b^2 = 1


This proves that  is equal to the complex conjugate of is equal to the complex conjugate of 
The steps to proving 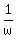 is equal to the conjugate of is equal to the conjugate of  are effectively the same as shown above. I'll let you do this part. are effectively the same as shown above. I'll let you do this part.
We'll use the fact that  along with along with  in part (b). in part (b).
==========================================================================
Part (b)
Let
x = complex conjugate of z = a-bi
y = complex conjugate of w = c-di
I'm using x and y instead of the overbar notation because I think the overbar notation is a bit clunky, especially when mixed with fraction bars.
So,
z+x = (a+bi)+(a-bi) = 2a
w+y = (c+di)+(c-di) = 2c
both are real values.
Furthermore,
z*x = 1
w*y = 1
was proven earlier in part (a), just with different notation.
This indicates that zx*wy = 1*1 = 1.
Now if
z = a+bi
w = c+di
Then,
z*w = (a+bi)*(c+di)
z*w = a*(c+di)+bi*(c+di)
z*w = ac+adi+bci+bdi^2
z*w = ac+adi+bci+bd(-1)
z*w = ac+adi+bci-bd
z*w = (ac-bd)+(adi+bci)
z*w = (ac-bd)+(ad+bc)i
Through very similar steps we can say,
x = a-bi
y = c-di
x*y = (ac-bd)-(ad+bc)i
As you can see:
zw+xy = [(ac-bd)+(ad+bc)i] + [(ac-bd)-(ad+bc)i]
zw+xy = [(ac-bd)+(ac-bd)]+[(ad+bc)i-(ad+bc)i]
zw+xy = [2(ac-bd)]+[0(ad+bc)i]
zw+xy = 2(ac-bd)+0i
zw+xy = 2(ac-bd)
which is a real result
To summarize everything so far for part (b), we can add any complex number to its conjugate to get a real result. Similarly, we can multiply any complex number with its conjugate to get a real result. Lastly, zw+xy sorta involves both concepts going on at once which means zw+xy is also a real number.
-------------------------
We build up those statements to be able to say the following
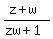
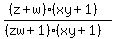 Multiply numerator and denominator by xy+1 Multiply numerator and denominator by xy+1
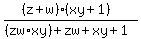 Expand out the denominator Expand out the denominator
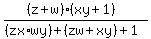 Group up the terms like such Group up the terms like such
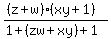 Plug in zx*wy = 1 Plug in zx*wy = 1
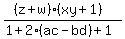 Plug in zw+xy = 2(ac-bd) Plug in zw+xy = 2(ac-bd)
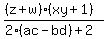 Simplify Simplify
The denominator 2(ac-bd)+2 is some real number. Let's expand out the numerator and see what we get
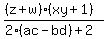
 FOIL the numerator FOIL the numerator
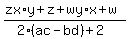
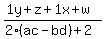 Plug in zx = 1 and wy = 1. Plug in zx = 1 and wy = 1.
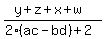
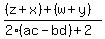 Group up the conjugate pairs Group up the conjugate pairs
 Plug in z+x = 2a and w+y = 2c Plug in z+x = 2a and w+y = 2c
The numerator 2a+2c is a real number.
We could divide every term by 2 to simplify further, but at this point we're effectively done with the proof.
Both the numerator and denominator are real values, so overall 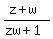 is a real number. is a real number.
Note: The condition  is to prevent the denominator is to prevent the denominator 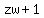 from being zero. from being zero.
Further Reading:
https://math.stackexchange.com/questions/427663/prove-if-z-w-1-and-1zw-neq-0-then-zw-over-1zw-is-a-real
|
|
|