Question 1171419: Hi
Bob and John had $540.00 altogether. Bob gave 1/7 of his money to John. In return John gave 1/4 of his total amount he had to Bob.Then they had both an equal amount of money.
How much did Bob have at first.
My solution is as follows B + J = 540
6/7B = 3/4J
upon solving the equation i get Bob $252 & John $288
however the book says that Bob had $210
Thanks
Answer by ikleyn(52903)   (Show Source): (Show Source):
You can put this solution on YOUR website! .
Bob and John had $540.00 altogether. Bob gave 1/7 of his money to John.
In return John gave 1/4 of his total amount he had to Bob.
Then they had both an equal amount of money.
How much did Bob have at first.
~~~~~~~~~~~~~~~~~~~~~
This problem is good to solve it by the BACKWARD method.
They started having $540 altogether.
The money did not get out and did not come from outside: they circulated inside.
The problem says that they finished having equal amounts.
Hence, at the end, Bob and John had $170, each.
Before it, John gave 1/4 of his total amount he had to Bob.
So, John left with 3/4 of the amount he has before it, which is $270
Hence, immediately before it, John had 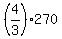 = 360 dollars,
and John gave 360/4 = 90 dollars to Bob.
Hence, when John had 360 dollars, Bob had 270-90 = 180 dollars.
Thus we completed one step back and found that before Bob gave 1/7 of his money to John,
they had $360 (John) and $180 (bob).
Now we know that after Bob gave 1/7 of his money to John, Bob left with 6/7 of his money, which is $180.
Hence, before this giving, Bob's initial money was = 360 dollars,
and John gave 360/4 = 90 dollars to Bob.
Hence, when John had 360 dollars, Bob had 270-90 = 180 dollars.
Thus we completed one step back and found that before Bob gave 1/7 of his money to John,
they had $360 (John) and $180 (bob).
Now we know that after Bob gave 1/7 of his money to John, Bob left with 6/7 of his money, which is $180.
Hence, before this giving, Bob's initial money was 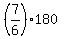 = $210.
Hence, John's initial money was $540 - $210 = $330.
ANSWER. Initially, Bob had $210, John had $330.
CHECK. (Bob, John) (Bob, John) (Bob, John)
(210, 330) ---> (210-30=180, 330+30=360) ---> (180+90=270, 360-90=270). ! correct ! = $210.
Hence, John's initial money was $540 - $210 = $330.
ANSWER. Initially, Bob had $210, John had $330.
CHECK. (Bob, John) (Bob, John) (Bob, John)
(210, 330) ---> (210-30=180, 330+30=360) ---> (180+90=270, 360-90=270). ! correct !
Solved mentally, without using equations, by the BACKWARD method.
|
|
|