Question 1171235: Hi
Jason spent 1/4 of his money and an extra $10 on some books. He the spent 2/5 of the remaining money plus an extra $8 on some dvds. If he was left with $130, how much money did he have at first.
Thanks
Found 4 solutions by greenestamps, josgarithmetic, Solver92311, MathTherapy:
Answer by greenestamps(13198)   (Show Source):
You can put this solution on YOUR website!
Let x be the amount he started with.
After spending 1/4 of his money, what he had left is  .
After spending an additional $10, what he had left is  .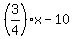
After he spent 2/5 of the remaining money, what he had left was  .
After spending an additional $8, the amount he had left was  .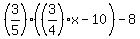
So solve the equation that says that amount is equal to $130:
 .
Hmmmmm.....!
Certainly do-able... but pretty ugly.
Below, I'm going to suggest a different way to find the answer. However, I recommend you go through the steps to solve the problem by solving that ugly equation.
---------------------------------------------
Now let's solve the problem by working backward.
He finished with $130; the last thing he did was spend an addition $8; so before that last $8 the amount he had left was $138.
Before the last $8, the thing he did previously was spend 2/5 of what he had. That means the $138 is 3/5 of what he had before; the previous amount he had was (5/3)($138) = $230.
Prior to that, he spent $10, so before that he had $240.
And the first thing he did was spend 1/4 or what he had originally, meaning the $240 is 3/4 of what he started with; the amount he started with was (4/3)($240) = $320.
-----------------------------------------------
If you went ahead and solved the problem by solving that earlier ugly equation, you should have found that in solving it you performed EXACTLY the same steps you did with the working-backward approach.
So the working backward approach is a much easier way to solve the problem, because a considerable amount of effort was required to come up with an algebraic equation to solve.
************************************************
Ignore the solution from tutor @josgarithmetic. The "extra" amounts spent DO come from the amount he started with.
"Solving" the problem by that tutor's method gives an original amount of money that is not a whole number, meaning his interpretation of the problem incorrect.
Answer by josgarithmetic(39615)  (Show Source):
Answer by Solver92311(821)  (Show Source):
Answer by MathTherapy(10551)  (Show Source):
|
|
|
