Question 1171228: I'm really stuck, please help? Thanks! Here's the question
A prime number is an integer greater than 1 with exactly two different positive factors, 1 and the number itself. There are three children in a family. Each of their ages is a prime number. The sum of their ages is 41 and at least two of the children have ages that differ by 16. Determine all possibilities for the ages of the children.
Found 3 solutions by math_tutor2020, greenestamps, MathLover1:
Answer by math_tutor2020(3817)   (Show Source): (Show Source):
You can put this solution on YOUR website!
Let a,b,c be the ages of the three children.
Since the ages are prime numbers, we can say
a > 1
b > 1
c > 1
which are all integers as well because the definition states "A prime number is an integer greater than 1".
The phrasing "at least two of the children have ages that differ by 16" means we have two cases:
Case A) Each child is separated by 16 years from their nearest neighbor
Case B) Only two children are separated by 16 years. The third child is closer than 16 years to one or both of the other siblings.
For now we'll focus on Case A.
Let's consider the case where each consecutive child is separated by 16 years from their nearest sibling
In other words,
gap from youngest to middle = 16 years
gap from middle to oldest = 16 years
In terms of algebra, this means:
a = b+16
b = c+16
where a > b > c. So 'a' is the oldest, b is the next oldest, and c is the youngest.
Adding those ages gets us
a+b+c = (b+16)+b+c
a+b+c = 2b+c+16
a+b+c = 2(c+16)+c+16
a+b+c = 2c+32+c+16
a+b+c = 3c+48
Set that equal to 41 and solve for c
3c+48 = 41
3c+48-48 = 41-48
3c = -7
3c/3 = -7/3
c = -7/3
We run into trouble. This solution doesn't satisfy c > 1 since it is negative. We don't even get a positive integer, which means even if we ignored the primeness restrictions, it's still not possible to have these three ages add to 41 (such that the gap conditions are set in place for case A).
Therefore, it's not possible to have such a scenario where each adjacent siblings have a gap of 16 years.
We can rule out Case A.
----------------------------------------------------------------------------
Since Case A has been ruled out, this must mean Case B is true.
So this must mean that exactly 2 children have a gap of 16 years between them.
Without loss of generality, let's say 'a' and b have that 16 year gap.
a = b+16
where child 'a' is older than child b
So a > b.
Add up the ages
a+b+c = 41
b+16+b+c = 41
2b+16+c = 41
2(b+8)+c = 41
In the last equation, the 2(b+8) is even since 2 is a factor.
If c were an even prime, aka c = 2, then 2(b+8)+c would be even as well.
Here's proof of that
2(b+8)+c = 2(b+8)+2 = 2(b+8+1) = 2*(some integer) = even number
But, this contradicts 41 on the right hand side being odd.
We must rule out c = 2.
So we must say that c is an odd prime. In other words, c > 2 is prime.
The list of odd primes less than 41 are: {3,5,7,11,13,17,19,23,29,31,37}
We will plug these items in for c to try to get a & b as primes.
Let's say c = 3
This means,
2(b+8)+c = 41
2(b+8)+3 = 41
2(b+8) = 38
b+8 = 19
b = 11
a = b+16 = 11+16 = 27
While the prime c = 3 does lead to the prime b = 11, we don't get a prime for a = 27 because 27 = 3*9.
This allows us to rule out c = 3 as well.
Let's try c = 5
2(b+8)+c = 41
2(b+8)+5 = 41
2(b+8) = 36
b+8 = 18
b = 10
we don't get a prime for b (because 10 = 2*5), so we stop here and cross c = 5 off the list.
Now try c = 7
2(b+8)+c = 41
2(b+8)+7 = 41
2(b+8) = 34
b+8 = 17
b = 9
This isn't prime either (9 = 3*3). Cross c = 7 off the list.
Now try c = 11
2(b+8)+c = 41
2(b+8)+11 = 41
2(b+8) = 30
b+8 = 15
b = 7 so far so good
a = b+16 = 7+16 = 23 this is prime as well
We finally get a,b,c all prime
(a,b,c) = (23,7,11) is one solution.
Any permutation of this list of three items is also a solution.
This means there are 3! = 3*2*1 = 6 different orderings of that triple and they are
(a,b,c) = (7,11,23)
(a,b,c) = (7,23,11)
(a,b,c) = (11,7,23)
(a,b,c) = (11,23,7)
(a,b,c) = (23,7,11)
(a,b,c) = (23,11,7)
For the sake of simplicity, we'll say  or or 
I would say  , but I want to be very clear that a = b = c is not possible (explained shortly below). So instead, I'm breaking it up into two cases. , but I want to be very clear that a = b = c is not possible (explained shortly below). So instead, I'm breaking it up into two cases.
So we'll make - 'a' the youngest (or possibly equal in age to their sibling b)
- then b is in the middle (possibly equal in age to 'a' or equal in age to sibling c, but b is not equal to both 'a' and c simultaneously)
- finally c is the oldest (but they could be equal in age to sibling b).
I realize that earlier I said a > b > c, which may seem confusing to flip the order now; however, I'm now realizing it's easier to list the smaller items first.
Note how a = b = c is not possible considering the gap of 16 years. A gap of any nonzero amount of time strongly implies that at least one of the ages must be different.
Also, if a = b = c were possible, then,
a+b+c = 41
a+a+a = 41
3a = 41
a = 41/3
but that isn't an integer, so it's definitely not prime either.
So again, a = b = c is not possible.
Go back to the solution we found earlier.
Based on  or or  , we get the triple (a,b,c) = (7,11,23) as one set of ages possible. , we get the triple (a,b,c) = (7,11,23) as one set of ages possible.
youngest = 7
middle = 11
oldest = 23
oldest - youngest = 23-7 = 16 year age gap
The gap from the middle to the youngest is 11-7 = 4 years; while the gap from the middle to the oldest is 23-11 = 12 years. Both of these gaps are not 16 years.
----------------------------------------------------------------------------
Let's keep going with higher c values
Try c = 13
2(b+8)+c = 41
2(b+8)+13 = 41
2(b+8) = 28
b+8 = 14
b = 6
6 isn't prime (6 = 2*3), so we move on.
Try c = 17
2(b+8)+c = 41
2(b+8)+17 = 41
2(b+8) = 24
b+8 = 12
b = 4
Not prime (4 = 2*2). Moving on.
Try c = 19
2(b+8)+c = 41
2(b+8)+19 = 41
2(b+8) = 22
b+8 = 11
b = 3 is prime
a = b+16 = 3+16 = 19 is also prime
We see that a,b,c are all prime.
We get another set of ages possible.
(a,b,c) = (19,3,19)
If we make  or or  , then (a,b,c) = (3,19,19). Here we have b = c = 19. , then (a,b,c) = (3,19,19). Here we have b = c = 19.
Again a = b = c is not possible.
So far we have two unique sets of solutions
(a,b,c) = (7,11,23)
(a,b,c) = (3,19,19)
----------------------------------------------------------------------------
As you can probably guess by now, we still have more c values to try out
Luckily, we're reaching the end.
Try c = 23
2(b+8)+c = 41
2(b+8)+23 = 41
2(b+8) = 18
b+8 = 9
b = 1
1 is not prime since b > 1 needs to be the case.
We can stop here.
Any larger prime c value will lead to 2(b+8)+c = 41 having a solution for b such that b > 1 is false.
Put another way: c < 23 must be the case for b > 1 to happen
Here's a proof of that
2(b+8)+c = 41
2(b+8) = 41-c
b+8 = (41-c)/2
b = (41-c)/2 - 8
We want b > 1, so,
b > 1
(41-c)/2 - 8 > 1
(41-c)/2 > 1+8
(41-c)/2 > 9
41-c > 9*2
41-c > 18
41 > 18+c
18+c < 41
c < 41-18
c < 23
Therefore, c < 23 is the upper bound. This means we don't have to check any more primes.
To summarize everything, we let
a = b+16
to show an age gap of 16 years between children 'a' and b
Then for c, we selected prime values from {3,5,7,11,13,17,19,23,29,31,37} and found that only c = 11 and c = 19 lead to a,b,c being all prime and that a+b+c = 41.
To help organize all the values, a table might be handy
| c | b | a | Are a,b,c prime? | | 3 | 11 | 27 | no, since a = 27 = 3*9 | | 5 | 10 | 26 | no, since b = 10 = 2*5 | | 7 | 9 | 25 | no, since b = 9 = 3*3 | | 11 | 7 | 23 | yes | | 13 | 6 | 22 | no, since b = 6 = 2*3 | | 17 | 4 | 20 | no, since b = 4 = 2*2 | | 19 | 3 | 19 | yes | | 23 | 1 | 17 | no, since b = 1 doesn't satisfy b > 1 |
I'm putting c first since we used values of c to generate corresponding b values, which lead to 'a' later on.
----------------------------------------------------------------------------
Answer:
There are two possible sets of ages
(a,b,c) = (7,11,23)
(a,b,c) = (3,19,19)
where  or or  and a,b,c are prime. and a,b,c are prime.
With the first set, we have the youngest (7) and oldest (23) separated by a gap of 16 years.
With the second set, we have two children equal to 19 years of age (but not all three are the same age).
As stated earlier, it is not possible to have all three children spaced out by 16 years.
Finally, a+b+c = 41 for both cases shown above.
Answer by greenestamps(13200)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There is nothing you can learn from having us work the problem for you. There is no algebraic method for finding the different possibilities; you just need to try different combinations in an orderly way.
The sum of the ages, 41, is an odd number; you can get an odd sum with three numbers either if two are even and one is odd, or if all three are odd. Since there is only one even prime number, the only possibilities are with three odd ages.
So search for them in an orderly way, by starting with the smallest possible age for the youngest.
I'll get you started and let you have the satisfaction of finding the answers yourself.
Suppose the youngest child's age is the smallest odd prime number, 3. Then the sum of the other two ages must be 38. Try the possibilities:
3+3+35 no; 35 is not prime
3+5+33 no; 33 is not prime
etc....
There may or may not be solutions with 3 as the age of the youngest. So next try 5 for the age of the youngest, meaning the sum of the other two ages is 36:
5+5+31 That is three prime numbers; but it doesn't satisfy the condition that two of the ages differ by 16.
5+7+29 Likewise....
5+11+25 no; 25 is not prime.
etc....
And after trying 5 as the age of the youngest, next try 7, then 11, ....
The requirement that two of the ages differ by 16 will mean you won't have very many combinations to look at to find the ones that satisfy all the conditions.
--------------------------------------------
Here is another approach to the problem that is probably faster than what is described above:
Start by looking for pairs of relatively small prime numbers whose difference is 16. There are probably very few such pairs, leading to a faster solution to the whole problem.
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are three children in a family. Each of their ages is a prime number.
let their ages be  , ,  , and , and 
if the sum of their ages is  , we have , we have
 ....eq.1 ....eq.1
and if at least two of the children have ages that differ by  , we have , we have

listing all the primes of  to to  we get: we get:
 , , , , , , , , , , , , , , , ,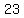 , , , ,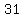 , , , ,
let’s separate primes who differ by 
 , ,
 , ,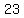
let’s consider this set as  , , : :
 ......substitute ......substitute  , , as as  , ,



hence,  , ,  , ,
 ......substitute ......substitute 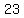 , , as as  , ,



hence,  , ,  , , 
|
|
|