Question 1171021: Let f ( x ) = ( x − 4 )^2
Find a domain on which f is one-to-one and non-decreasing.
Find the inverse of f restricted to this domain f ^-1 ( x ) =
Answer by MathLover1(20849)   (Show Source):
You can put this solution on YOUR website!
The original function  is
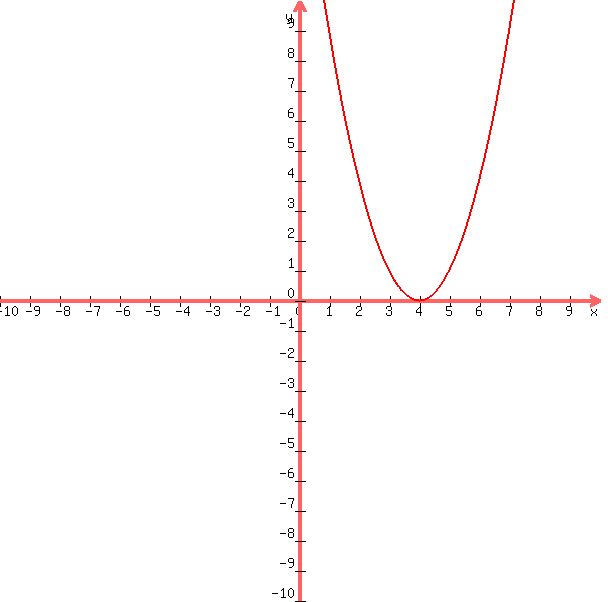
and it is  one-to-one, but the function is restricted to a domain of  or  on which it  one-to-one.
see parts separately:
To find the inverse, start by replacing  with the simple variable  .
 ............interchange  and
 ..........take square root
This is not a function as written. We need to examine the restrictions on the domain of the original function to determine the inverse. Since we reversed the roles of and for the original , we looked at the domain: the values could assume. When we reversed the roles of and , this gave us the values could assume. For this function,  , so for the inverse, we should have  , which is what our inverse function gives.
1. The domain of the original function was restricted to , so the outputs of the inverse need to be the same,  , and we must use the + case:
2. The domain of the original function was restricted to  , so the outputs of the inverse need to be the same,  , and we must use the - case:
analysis of the solution
On the graphs below, we see the original function graphed on the same set of axes as its inverse function. Notice that together the graphs show symmetry about the line  . The coordinate pair ( , ) is on the graph of and the coordinate pair(,) is on the graph of  .
For any coordinate pair, if ( ,  ) is on the graph of , then (, ) is on the graph of .
Finally, observe that the graph of intersects the graph of on the line  .
Points of intersection for the graphs of and will always lie on the line .
|
|
|
