Question 1170895: Foci at (2, 3) and (2, -1), endpoint of minor axis (4, 1). Find the equation of the ellipse and sketch the graph.
Found 2 solutions by MathLover1, greenestamps:
Answer by MathLover1(20850)   (Show Source): (Show Source):
You can put this solution on YOUR website! Equation of the ellipse in standard form:
 ...horizontal major axis ( ...horizontal major axis ( ) )
 ...vertical major axis ( ...vertical major axis ( ) )
given Co-vertices:( , , )->means we have )->means we have 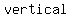 major axis major axis
so, you need

given foci at ( , , ) and ( ) and ( , , ) )
then center is half way between
center: ( , , )=( )=( , , ) )
distance between foci and center is  and -> and -> 
Co-vertices: given one at ( , , ) )
distance from center ( , , ) is ) is 
the other one is at ( , , ) same distance from center ) same distance from center
(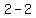 , , )=( )=( , , ) )
Minor axis length: 
Semiminor axis length: 
now we can calculate 



then your equation is:


Answer by greenestamps(13203)   (Show Source): (Show Source):
You can put this solution on YOUR website!
The two foci are on the same vertical line, so the major axis is vertical. The standard form of the equation is then

The center (h,k) is at (2,1) -- halfway between the two foci; a is the semi-major axis and b is the semi-minor axis.
The semi-minor b is the distance from the center (2,1) to the given point (4,1), so b=2.
The distance from the center to each focus is c, where a, b, and c are related by

The distance from the center to each focus is 2, so c=2. Then



Now we have the center (h,k), and we know a^2 and b^2, so we have all we need to write the equation:

|
|
|